[알고리즘으로 단단해지기] 1.Prologue
알고리즘
-
알고리즘은 다섯 가지의 task를 따른다.
-
Input
-
Output
-
- Definiteness
- 실행했을 때 다른 해석의 여지가 없어야 한다.
- Finiteness
- 반드시 유한한 횟수의 연산으로 결과를 만들어야 한다.
- Efficiency
- 컴퓨터의 자원을 최대한 절약하면서 결과를 만들어야한다.
Computational complexity (계산 복잡도)
- Solution
- 솔루션은 항상 존재해야 한다.
- Cost
- 입력에 드는 Resource는 시간적(temporal) + 공간적(spatial)자원이다.
- temporal resource: CPU
- spatial resource: memory
- 입력에 드는 Resource는 시간적(temporal) + 공간적(spatial)자원이다.
- 계산 복잡도의 중요한 점
- 최악의 경우의 성능이 중요하다.
- 시간의 성능이 중요하다.
-
성능은 입력의 크기 $n_0 < n_1$ → $f(n_0) \leq f(n_1)$에 따른다.
- 매우 큰 입력이 중요하다.
-
Example of $f(n): O(n), Ω(n), Θ(n)$
- Asymtotic(점근) upper bound: $O(n)$ → Worst case
- Asymptotic lower bound: $Ω(n)$ → Best case
- Asymptotic tight bound: $Θ(n)$ → Exact case
-
- 몇개의 주요 함수는 표준으로 사용된다.
- 최악의 경우에서 f(n)은 g(n)보다 더 좋아야 한다.
-
g(n)
- 측정의 표준 f(n)에 대한 보장이다.
- O()표기법에 의해 1, n, logn, n^2, nlogn, n^n등으로 표기한다.
- g(n)은 f(n)의 upper bound이다.
-
- 최악의 경우에서 f(n)은 g(n)보다 더 좋아야 한다.
Big-O Notation
-
알고리즘의 시간 복잡도를 계산하기 위해 빅오($O$) 표기법을 사용한다.
-
빅오 표기법은 다음과 같은 수식으로 표현한다.
-
$f(n)$ is $O(g(n))$ as $n$ → $∞$, if and only if $\exist\(n_0$, $\exists\)M > 0$ such that $ f(n) \leq M g(n) $ for $n > n_0$ -
위 공식을 따라 f(n)=O(g(n))으로 표시 가능하다.
-
다음은 아래와 같이 말할 수 있다.
- $f(n)$은 $g(n)$보다 빠르다.
- $f(n)$은 $g(n)$보다 성능이 좋다.
- $f(n)$의 upper bound는 $g(n)$이다.
- $f(n)$의 최악의 성능은 $g(n)$이다.
- $g(n)$은 $f(n)$보다 느리다.
- $g(n)$은 $f(n)$보다 성능이 나쁘다.
- $g(n)$은 $f(n)$의 보장이다.
- 아래와 같은 그래프와 수식이 있을 때 $=$ 등호는 같다보다 포함 관계로 해석한다.
- $f(n)=O(g(n))$
- $f(n)=O(h(n))$
- $f(n)=O(k(n))$
-
이유: 등호를 ‘같다’ 라고 할 시 $O(g(n)) \neq O(h(n))$이 되기 때문이다.
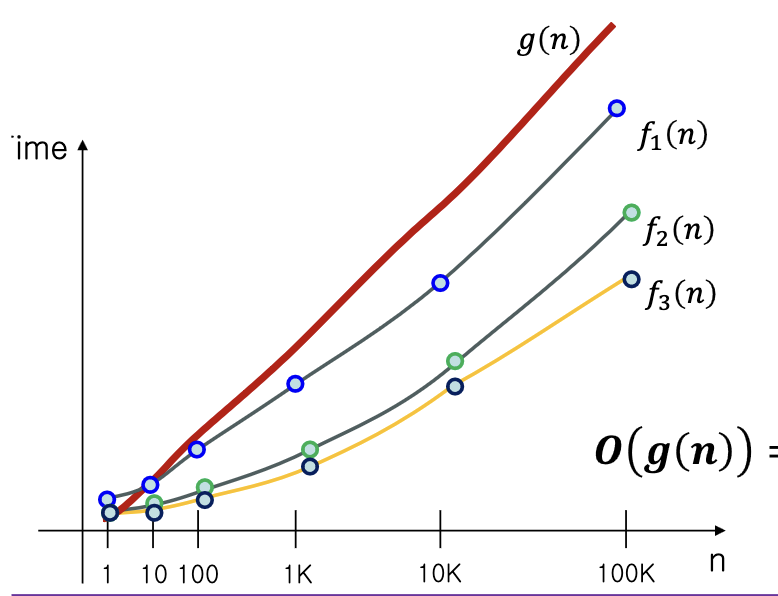
- 아래와 같은 그래프에서 집합의 관계를 따질 수 있다.
- $f_1(n) = O(g(n))$
- $f_2(n) = O(g(n))$
- $f_3(n) = O(g(n))$
- $O(g(n)) = {f_1(n),f_2(n),f_3(n)}$
- $O(g(n))$역시 하나의 집합이다.
-
$f(n) = n^2$과 $g(n) = n^2+n+4$의 관계를 증명하고자 한다.
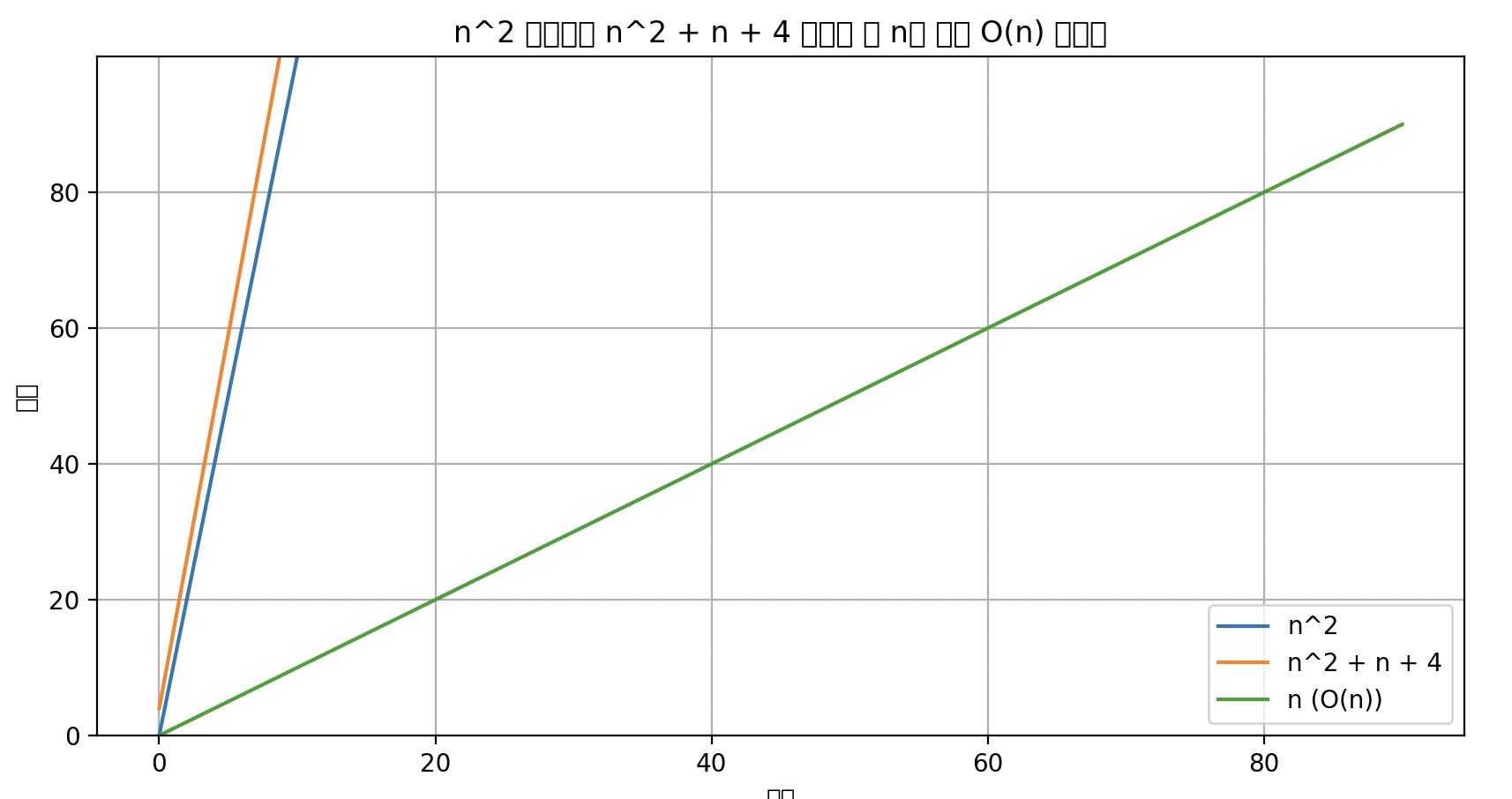
- $f(n) = O(g(n))$ 인가? 를 증명하기 위해선 아래와 같이 증명해야 한다.
- 위 문제를 증명하려면 $”\exists M, n_0, f(n) \leq Mg(n)$, for $n\geq n_0”$을 만족하는 $M$과 $n_0$가 존재함을 증명해야 한다.
- $n^2 \leq M(n^2+n+4)$를 만족하는 $M$과 $n_0$는?
- $M=1$, $n_0=1$이면 가능하다.
- 이렇듯 시간 복잡도를 증명할 수 있음. 중요하다!
- 마찬가지로 $g(n)=O(f(n))$을 증명해보자.
- $”\exists M, n_0, f(n) \leq Mg(n)$, for $n\geq n_0”$을 만족하는 $M$과 $n_0$가 존재함을 증명해야 한다.
- $n^2+n+4\leq Mn^2$을 만족하는 $M$과 $n_0$은?
- $M=3,\text{ }n_0=2$면 가능하다.
- 즉, 위 수식에 대한 관계는 아래와 같다.
- $f(n) = O(g(n))$
- $g(n)=O(f(n))$
- $f(n)=O(g(n))$ 이고 $g(n) = O(f(n))$
- $f(n)=\Omega (g(n))$
- $f(n)=\Theta (g(n))$
- $g(n)=\Omega (f(n))$
- $g(n)=\Theta (f(n))$
-
-
$f(n) = O(g(n))$이라면 $g(n) = \Omega (f(n))$, if $g(n) \geq Mf(n)$

- $f(n) = O(g(n))$ and $f(n)=\Omega (g(n))$일 때는
- $f(n)\leq Mg(n)$ and $f(n)\geq Mg(n)$이다.
- $f(n)=\Theta (g(n))$도 충족한다.
- $f(n)$과 $g(n)$은 같은 비율로 증가한다.
일반 빅오 함수들의 시간 복잡도
- 시간 복잡도 성능을 나타내는 빅오 표기법으로 알고리즘의 단계를 기호화 시킬 수 있다.
- Constant time : $O(1)$
- Linear Time: $O(n)$
- Polynomial time: $O(n^k)$
- $O(log\text{ } n)$
- $O(n\text{ }log\text{ }n)$
- NP-complete: $O(K^n)$, $O(n^n)$
- 다음의 순서를 따른다.
- $O(1) < O(log\text{ }n) < O(n) < O(n\text{ }log\text{ }n) < O(n^k) < O(k^n) < O(n^n)$
Constant time $O(1)$
- $f(n) = O(g(n))=O(1)$ → constant time
- $g(n)=1$
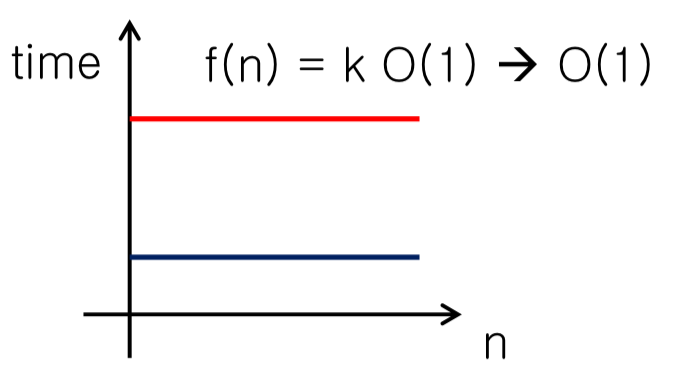
- 입력($n)$과 비례하다.
- $n$이 1이면 1, $n$이 100이면 100이다.
void print_name (char *name) {
printf("%s\n", name);
}
Linear time $O(n)$
- $f(n)=O(g(n))=O(n)$ → linear time
- $g(n)=n$
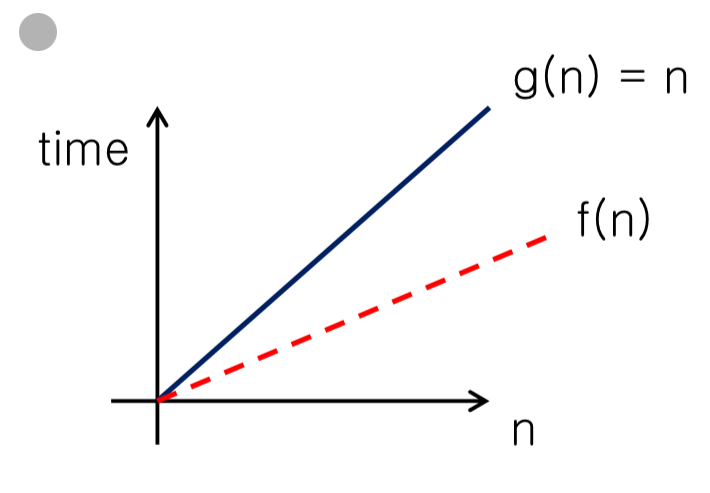
- 실행 단계가 n번이다.
void func (int n) {
i = 0;
while (i < n) {
Read A[i];
i++;
}
}
Polynomial time $O(n^k)$
- $f(n) = O(g(n)) = O(n^k)$ → polynomial time
- $g(n) = n^k$
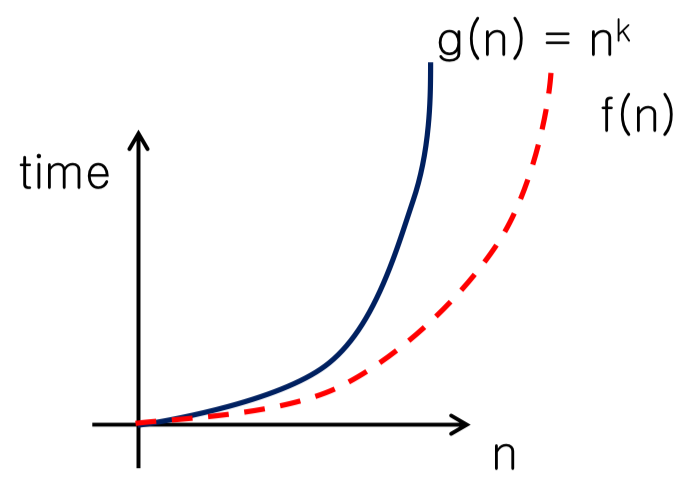
- 실행의 단계가 $n^k$번 dlek.
- for문의 중첩에 따라 대체로 제곱이라고 생각하면 된다.
- 이중 for문이기 때문에 $O(n^2)$의 시간복잡도를 갖는다.
void func (int n) { for (int i = 0; i < n; i++) { for (int j = 0; j < n; j++) { Read A[i, j]; Wrtie A[i, j]; } } }
Log-n time $O(log\text{ }n)$
- $f(n) = O(g(n))=O(log\text{ }n)$ → log-n time
- $g(n)=log\text{ }n$
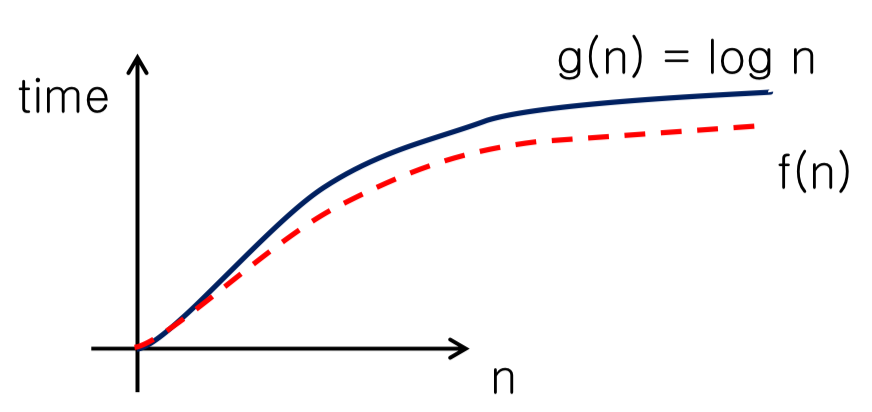
- 실행의 단계가 $log\text{ }n$번 이다.
- i를 매 루프마다 10씩 곱하고 있으므로, $log_{10}\text{ }n$만큼 걸린다.
- 빅오는 상수는 버리기 때문에 $O(log\text{ }n)$으로 표기한다.
- i를 매 루프마다 10씩 곱하고 있으므로, $log_{10}\text{ }n$만큼 걸린다.
void func (int n) {
for (int i = 0; i < n; i*=10) {
Read A[i, j];
Write A[i, j];
}
}
- 위 코드의 실행 순서는 다음과 같다.
| $n$ | 1 | 10 | 100 | 1,000 | 10,000 | 100,000 |
|---|---|---|---|---|---|---|
| $f(n)$ | 1 | 2 | 3 | 4 | 5 | 6 |
- 대표적으로 Binary Search(이진 탐색)이 대표적인 $O(log\text{ }n)$ 알고리즘이다.
int BS(int x, int n, int S[]) {
if (n == 1)
return (S[0] == x);
if (x > S[n/2]
return BS(x, n/2, S[n/2+1, ..., n-1]);
else
return BS(x, n/2, S[0, ..., n/2]);
n log-n time $O(n\text{ }log\text{ }n)$
- $f(n) = O(g(n)) = O(n\text{ }log\text{ }n)$ → n log-n time
- $g(n)=n\text{ }log\text{ }n$
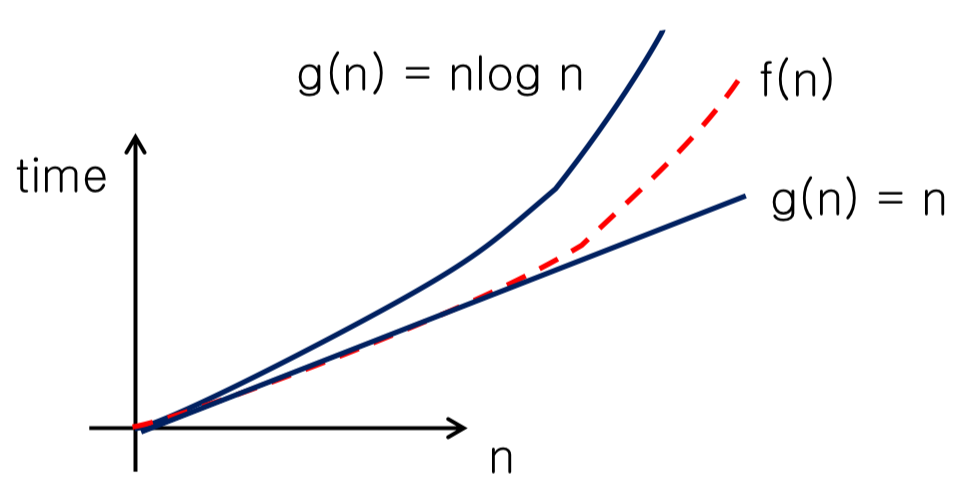
- 실행 단계가 $n\text{ }log\text{ }n$ 이다.
- 코드를 보면 외부 for문은
n번만큼 반복하며, 내부 for문은 n까지j*=2만큼 반복한다.j*=2만큼 반복한다는 것은 $O(log\text{ }n)$의 시간복잡도를 의미한다.- 외부 for문은 $O(n)$만큼 반복하므로, 둘이 동시에 실행 시 $O(n\text{ }log\text{ }n)$의 반복횟수가 된다.
- 코드를 보면 외부 for문은
void func (int n) {
for(int i = 1; i <= n; i++) {
for(int j = 1; j <= n; j*=2) {
Read A[i, j];
Write A[i, j];
}
}
}
- $O(n\text{ }log\text{ }n)$은 대체로 보기 힘든 시간복잡도이나, Merge Sort(병합 정렬)이 이 알고리즘이다.
void MergeSort(int n, int S[]) {
if (n > 1) {
MergeSort(n/2, s[0, ..., n/2 -1]);
MergeSort(n/2, s[n/2, ..., n-1]);
Merge(n,s);
}
}
Exponential time $O(k^n)$
- $f(n)=O(k^n)$ → exponential time
- $g(n)=k^n$
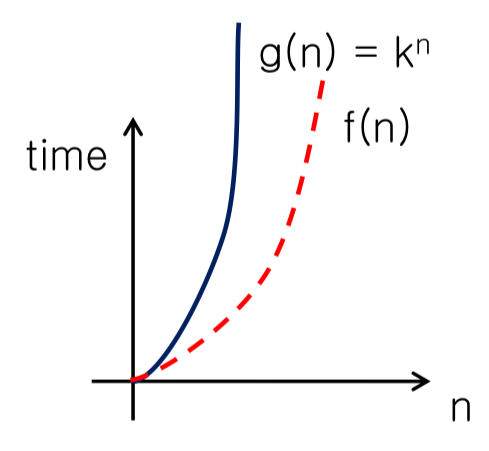
- 실행 단계가 $k^n$번 이다.
- 아래 코드는 피보나치 수열을 재귀로 푼 코드인데, $k^n$번 반복하는 최악의 알고리즘이다.
- 아래와 같은 시간 복잡도를 가지는 알고리즘들을 NP-complete 알고리즘이라 한다.
- $g(n)=k^n$
- $g(n)=n^n$
- $g(n)=n!$
int Fib(int n) {
if(n==0) return 0;
if(n==1) return 1;
return Fib(n-1) + Fib(n-2);
}
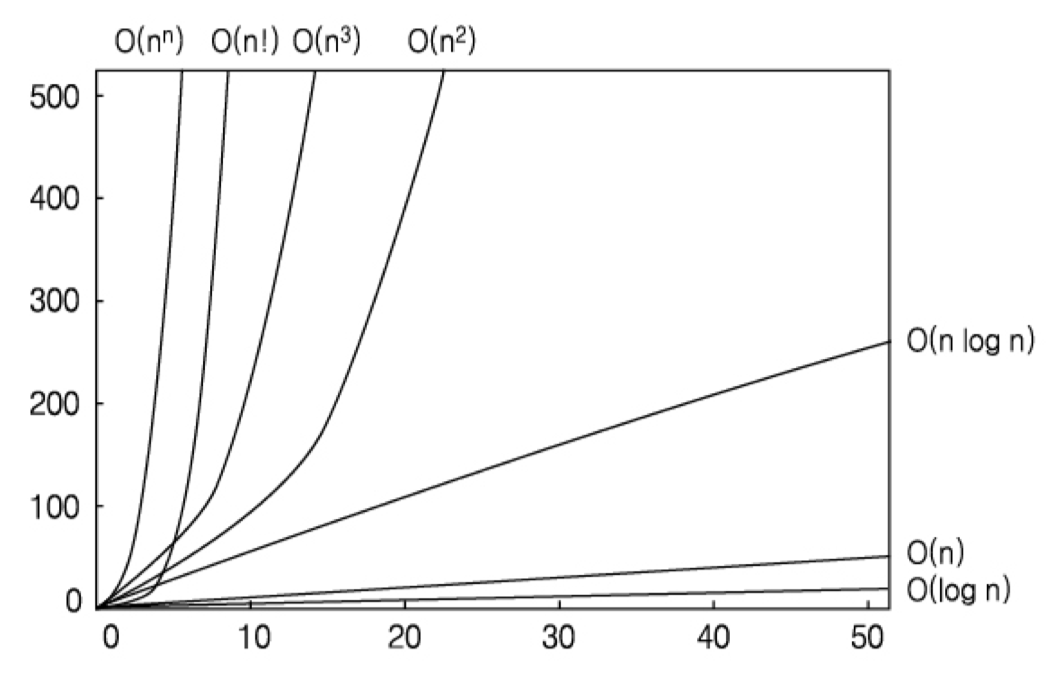
Comparsion
- 보다시피 각 알고리즘마다 시간의 차이가 입력량($n$)에 따라 기하급수적으로 달라진다.
- 만약 $O(n^2)$ 알고리즘을 $O(n)$ 알고리즘으로 바꾼다면, 정말 대단한 것이다.
- 참고로, $O(1)$이 가장 빠르다. $x$축과 겹치기 때문에 표기하지 않았다.
알고리즘의 목적
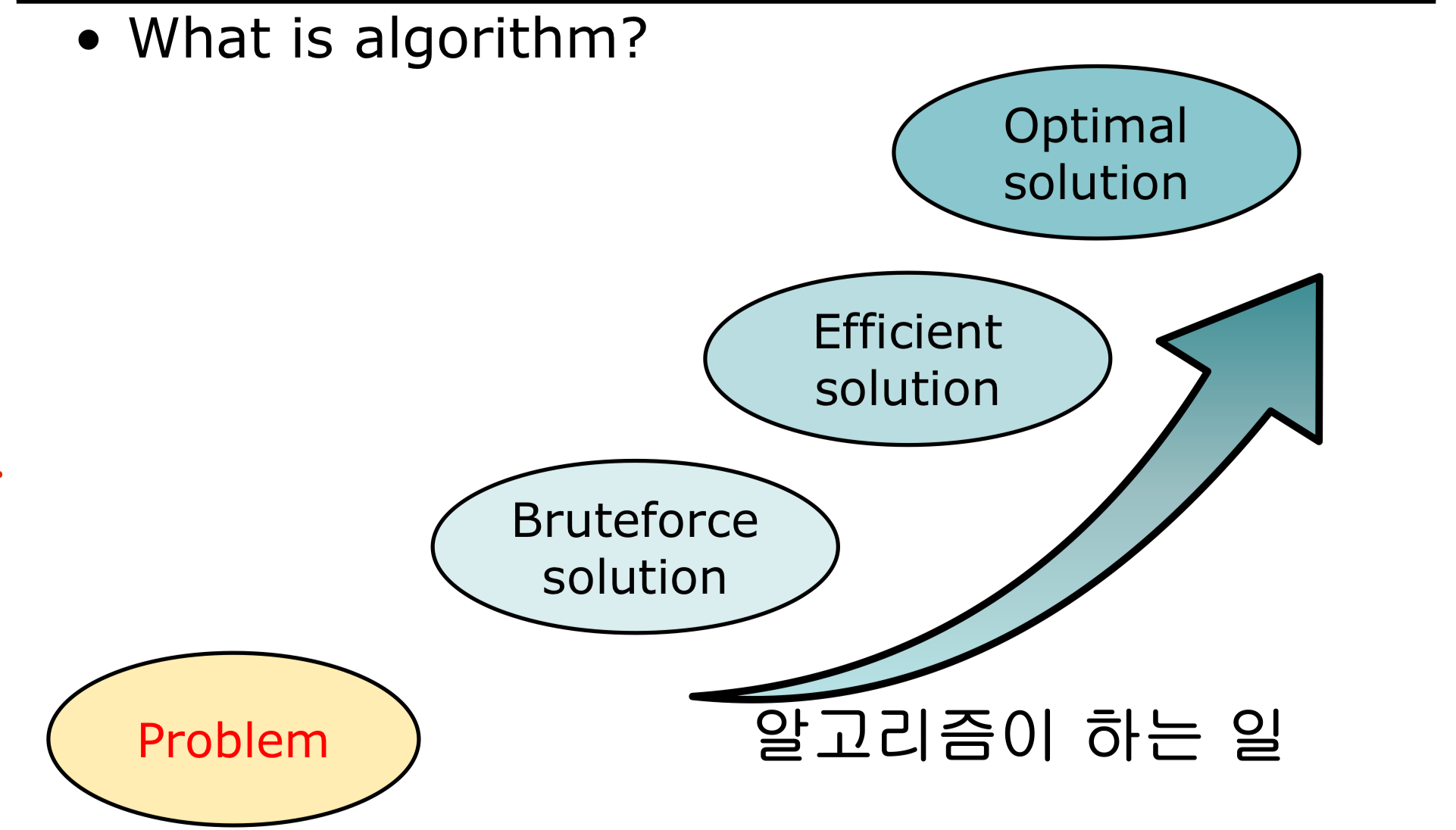
- Bruteforce solution
- 무작정 대입으로 결과는 도출하나, 성능은 최악이다.
- Efficient solution
- 효율적인 알고리즘 솔루션이다.
- Optimal solution
- 정석으로 받아들여질 알고리즘이다.
Recurrence relation
Why recurrence relation?
- 점화식(recurrence relation)은 수열에서 각각의 항들의 관계를 나타낸 식이다.
- 점화식을 통해 시간복잡도를 풀기 위해선 일반항($a_n$)이 필요하다.
-
점화식은 $a_{n+1} = f(a_n)$처럼 생겼다.
-
예시로 피보나치 수열을 $O(n^k)$ 시간복잡도를 가지는 재귀로 만들었다면, 아래와 같이 식을 적을 수 있다.
- 이를 점화식으로 나타낸다면 $a_n-a_n-1 = 2$ 이다.
$T(n)=T(n=1)+T(n-2)+k$
- 이 식에서 이다. 코드 상의 기저 조건을 나타낸다.
- 기저 조건은
if (n==0…부분이다. 재귀가 끝나는 조건이라 생각하면 된다.
- 기저 조건은
int Fib(int n) { if (n==0 || n==1) { return n; } return Fib(n-1) + Fib(n-2); } -
Solution
이를 풀기 위해 세 가지의 방법이 있다.
- 특정방정식(Characteristic equation)
- 반복대입법(Repeated substitution or telescoping)
- 마스터정리(Master theorem)
Characteristic equation (특정방정식)
- $t_n$을 $x_n$으로 대체한 recurrence relation으로부터 생성된 equation이다.
- 특정방정식은 두 종류로 나뉜다.
- 동일항 점화식 (Homogeneous recurrence relation)
-
모든 항이 동일한 점화식. (ex. 모든 항이 $t_n$이다.)

-
- 비동일화 점화식 (Inhomogeneous recurrence relation)
- 모든 항이 동일하지 않은 점화식이다.
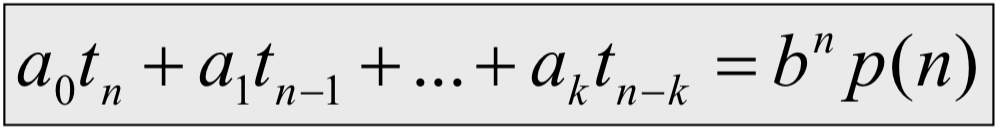
- 동일항 점화식 (Homogeneous recurrence relation)
Homogeneous recurrence relation
- 풀이 전략!
- 특정 다항식 만들기
- $t_n$을 $x_n$으로 치환하라.
- $a_0t_n+a_1t_{n-1}+…+a_kt_{n-k}=0$ → $a_0x^n+a_1x^{n-1}+…+a_kx^{n-k}=0$
- 특정 다항식 풀기
- $x^{n-k}(a_0x^n+a_1x^{n-1}+…+a_kx^{n-k})=0$
- → $a_0x^k+a_1x^{k-1}+…+a_k=0$
- → Solution: $r_1, r_2,…,r_k$
- recurrence relation의 해
- $t_n=\sum ^k_{i=1}c_ir^n_i$
- 특정 다항식 만들기
Examples
- Example 1 :
$t_n-3t_{n-1}-4t_{n-2}=0,\text{ }n\geq2,t_0=0,t_1=1.$
- 풀이
- 특정 다항식 만들기
- $x^n-3x^{n-1}-4x^{n-2}=0$$x^n-3^{x-1}-4x^{n-2}=0$
- 특정 다항식 풀기
- $(x^n-3x^{n-1}-4x^{n-2})/x^{n-2}=0$
- → $x^2-3x-4=0$
- → $(x-4)(x+1)=0$
- $\therefore x=4,x=-1$
- recurrence relation의 해
- $t_n=\sum^k_{i=1} c_ir^n_i$에 따라
- $t_n = C_1(4)^n+C_2(-1)^n$
- 여기서 $t_0 = 0,t_1=1$이란 조건이 주어졌으므로,
- $t_0=C_1(4)^0+C_2(-1)^0=0$
- $t_0=C_1+C_2=0$ $\therefore C_1=-C_2$
- $t_1=C_1(4)^1+C_2(-1)^1=1$
- $\therefore -(4C_2)+-C_2 = 1$
- → $-5C_2 = 1$
- $\therefore C_1 = \frac{1}{5}$, $C_2 = -\frac{1}{5}$
- $C_1+C_2=0$ 이므로, $C_1=\frac{1}{5}$ 임.
- $t_n=\frac{1}{5}(4)^n-\frac{1}{5}(-1)^n$
- → $t_n=\frac{1}{5}{(4)^n-(-1)^n)}$
- Example 2 :
$t_n=t_{n-1}+t_{n-2},\text{ }n\geq 2,\text{ }t_0=0,t_1=1$
- 풀이
- 특정 다항식 만들기
- $x^n=x^{n-1}+x^{n-2}$
- → $x^n-x^{n-1}-x^{n-2}=0$
- 특정 다항식 풀기
- $(x^n-x^{n-1}-x^{n-2})/x^{n-2}=0$
- → $x^2-x-1=0$
- 근의 공식($\frac{-b \pm \sqrt{b^2 -4ac};}{2a}$)에 따라 아래와 같이 해를 구함
- $\therefore x=\frac{1 + \sqrt{5}}{2}$, $x=\frac{1 - \sqrt{5}}{2}$
- recurrence relation의 해
- $t_n=\sum^k_{i=1} c_ir^n_i$에 따라
- $t_n=C_1(\frac{1 + \sqrt{5}}{2})^n + C_2(\frac{1 - \sqrt{5}}{2})^n$
- $t_0=C_1+C_2=0$ $\therefore C_1=-C_2$
- $t_1=C_1(\frac{1+\sqrt5}{2}) + C_2(\frac{1-\sqrt5}{2})=1$
- → $t_1=-C_2(\frac{1+\sqrt5}{2}) + C_2(\frac{1-\sqrt5}{2})=1$
- → $t_1=C_2(\frac{-1-\sqrt5 + 1-\sqrt5}{2})=1$
- → $t_1=C_2-\sqrt5=1$
- →$t_1=C_2=-\frac{\sqrt5}{5}$ $\therefore C_1=\frac{\sqrt5}{5}, C_2=-\frac{\sqrt5}{5}$
- $t_n=\frac{\sqrt5}{5}(\frac{1+\sqrt5}{2})^n-\frac{\sqrt5}{5}(\frac{1 - \sqrt{5}}{2})^n$
- →
Inhomogeneous recurrence relation
- homogeneous 형식으로 바꾼 후 $C_1$과 $C_2$값을 구해라.
Cases
- Case 1 :
$t_n-2t_{n-1}=3^n$
- Inhomogeneous → Homogeneous로 하기위해 $3^n$을 제거해야 한다.
- 기본 식에 $n=n+1$를 대입함
- → $t_{n+1}-2t_n=3^{n+1}$
- → $t_{n+1}-2t_n=3*3^n$
- 기본 식에 $3^1$을 곱함
- $3t_n-6_{n-1}=3*3^n$
- 우변을 0으로 만들기 위해 두 식을 뺀다.
- $t_{n+1}-5t_n+6_{n-1}=0$
- 이후 homogeneous방식으로 $t_n$을 구하면 된다.
- Case 2 :
$t_n-2t_{n-1}=(n+5)3^n$
- Inhomogeneous → Homogeneous로 하기위해 $3^n$을 제거해야 한다.
- 기본 식에 $n=n+2$를 대입함
- → $t_{n+2}-2t_{n+1}=(n+7)3^{n+2}$
- 기본 식에 $3^2$인 9를 곱함.
- → $9t_n-18t_{n-1}=(n+5)3^{n+2}$
- 우변을 0으로 만들기 위해선 두 식을 더한 값을 빼야 함.
- $(n+7)3^{n+2} + (n+5)3^{n+2}$를 먼저 함.
- → $3(n+7)3^{n+1}+3(n+5)^{n+2}$
- → $6(n+6)3^{n+1}$ 로 정리
- 기존 식에서 우변을 $6(n+6)3^{n+1}$ 로 만들기 위해 $-6$과 $n=n+1$을 대입함.
- $-6t_{n+1}+12t_n=-6(n+6)3^{n+1}$
- $(n+7)3^{n+2} + (n+5)3^{n+2}$를 먼저 함.
- 세 식을 모두 더해 homogeneous화 시킴.
- $1.+2.+3.$
- → $t_{n+2}-8t_{n+1}+21t_n-18t_{n-1}=0$
- $1.+2.+3.$
Repeated Substitution (반복 치환)
- 우변에 연속적인 recurrence relation이 있다.
- value는 원래 equation으로 치환, 이전 버전의 equation 도출한다.
- $T(n)$은 $n$개의 input을 처리할 때 걸리는 시간이다.
Examples
$T(n)=2T(n/2)+n,\text{ }T(1)=1$
- Merge Sort(병합정렬)의 공식과 동일하다.
- 전부 탐색하는데, 기준에 따라 반반 나누는 식이다.
- 아래 그림처럼 해결이 가능하나, 이는 Matser theorem으로 쉽게 풀 수 있다.

Master theorem
-
만약 $T(n)=aT(\frac{n}{b})+O(n^d)$ 형식이고, $a>0, b>1,g\geq0$일 때 아래 공식이 성립함.
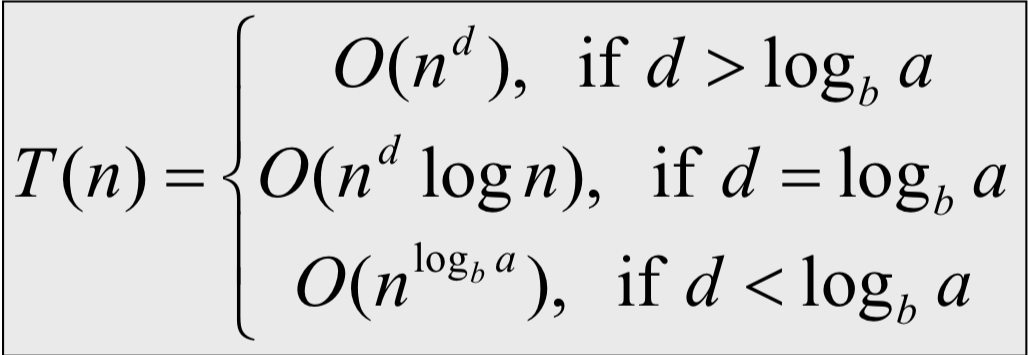
- $O(n^d)$일 경우 나누는 시간이 더 든다는 뜻이다.
- $O(n^d\text{ }log\text{ }n)$일 경우 나누는 시간과 푸는 시간이 같다는 뜻이다.
- $O(b^{log_b\text{ }a})$일 경우 푸는 시간이 더 든다는 뜻이다.
Examples
$T(n)=2T(n/2)+n$
-
Merge Sort이다.
- 위 식에서 a, b, d는 아래와 같다.
- $a=2,b=2,d=1$
-
Master theorem에 따르면 $1 = log_2\text{ }2$이므로, 위 식의 시간복잡도는 $O(n \text{ }log\text{ }n)$이다.
-
n명중에 성별로 나눠 성적 1등이 누구인지를 찾을 때 시간복잡도가 얼마나 걸리는지를 확인해보자.
- $T(n)=2T(\frac{n}{2})+O(1)$로 식을 표시할 수 있다.
- $O(n)$이 아니고 $O(1)$인 이유는 여, 남으로 $2T(\frac{n}{2})$로 나눴으면 일일이 한명에게 물어보지 않아도 된다.
- 여, 남으로 정렬 후 성별의 1등끼리 비교하면 사람이 아무리 많아져도 2단계밖에 안걸린다.
- $O(n)$이 아니고 $O(1)$인 이유는 여, 남으로 $2T(\frac{n}{2})$로 나눴으면 일일이 한명에게 물어보지 않아도 된다.
-
즉, $a=2, b=2,d=0$으로 구할 수 있다.
- Master theorem에 따라, $0<log_2\text{ }2$이므로, $O(n^{log_2\text{ }2})=O(n)$의 시간복잡도를 가진다 할 수 있다.
Fibonacci (피보나치)
- 피보나치 수열이란 $f(n)=f(n-1)+f(n-2)(^{f(0)=0}_{f(1)=1} (n\geq2)$이다.
- 예시로, 달마다 토끼의 수를 들 수 있다.
Fibonacci Problem
- 피보나치 수열을 어떻게 계산할까?
- n번째 피보나치 수열은 무엇일까?
Fibonacci Solution
- Simple and intutive(간단하고 직관적)이지만, 효율적이지 않다.
- → bruteforce algorithm
- Simple and efficent(간단하고 효율적)이지만, 개선이 가능하다.
-
More efficient → Optiomal algorithm
- Solution 1 : A recursive call (재귀 호출)
- 아래 코드처럼 재귀함수로 피보나치 수열을 돌릴 수 있다.
int Fib(int n) {
if(n == 0 || n == 1) {
return n;
return Fib(n-1) + Fib(n-2);
}
- 다만, 이 코드의 시간복잡도는 $O(2^n)$이다.. == Bruteforce algorithm.
- Solution 2: An iterative approach (반복 호출)
- 아래 코드처럼 for문으로 피보나치를 짜면 $O(n)$의 시간복잡도를 가진다.
int Fib_interative(int n) {
int FS[n+1];
FS[0] = 0;
FS[1] = 1;
for(int i = 2; i <= n; i++) {
FS[i] = FS[i-1] + FS[i-2];
}
return FS[n];
- $O(n)$ 시간복잡도를 가지는 알고리즘이긴 하나, 더 효율적으로 개선이 가능하다.
- Solution 3: A divide-and-conquer approach (분할 정복 접근)
- 아래와 같이 실행시키면 $O(log\text{ }n)$의 시간복잡도를 가진다.
- $i = i * i$이므로, 4..16..64…와 같이 급격히 증가함. 매우 효율적인 알고리즘이다.
int get_k_n(int k, int n) {
int i;
int kn;
for(i = 2; kn = k; i <= n; i = i * i) {
kn = kn * kn;
}
return kn;
- 피보나치 수열은 다르게도 풀 수 있다.
int get_k_n (int k, int n) {
int i;
int kn;
for(i = 1; kn = 1; i <= n; i = i + 1) {
kn = k * kn;
}
return kn;
}
- 이 코드의 시간 복잡도는 $O(n)$이다.
- 제곱승 구하는 알고리즘에 iterator, for 문을 쓴 경우 $n$의 크기에 따라 성능이 크게 좌우되므로 좋은 알고리즘은 아니다.
- 아래 코드와 같이 풀 수도 있다.
int get_k_n(int k, int n) {
if (n == 0) {
return 1;
}
if (n == 1) {
return k;
int kn = get_k_n(k, n/2);
return kn * kn;
}
- 이 코드의 시간복잡도는 $O(log\text{ }n)$이다. 매우 효율적인 알고리즘이다.
- $T(n)=T(\frac{n}{2})+1$으로 풀 수 있다.
- $T(n)$은 재귀호출의 시간 복잡도를 따질 때 가장 중요하다.
- Master theorem으로 풀어보면
- $a=1,n=2,d=0$이므로,
- $0 = log_2\text{ }1$이므로,
- $\therefore O(log\text{ }n)$의 시간복잡도를 가진다.
- $T(n)=T(\frac{n}{2})+1$으로 풀 수 있다.
댓글남기기