[알고리즘으로 단단해지기] 2.Divide & Conquer (분할 정복)
Divide & Conquer (분할 정복)
- 분할 정복은 주어진 $n$개의 집합을 $k$개의 집합으로 나눠 문제를 해결하는 알고리즘 기법이다.
Three Key Points of Divide & Conquer
- Divide
- 문제를 풀기 쉽도록 잘게 자른다.
- Conquer
- 자른 문제를 재귀적으로 해결한다.
- Combine (Optional)
- Conquer한 내용을 결합해 결과를 도출한다.
- Optional로 상황에 따라 없어도 되는 단계이다.
Three Check Point of Divide & Conquer
- Same format
- 입력과 반환이 매 순간 항상 같아야 한다.
- Reduced problem size
- 재귀를 호출하는 입력은 점점 작아져야 한다.
- Degenerate case
- 충분히 작은 크기일 때 반드시 재귀를 빠져나갈 수 있는 예외 조건이 있어야 한다.
Most Divide & Conquer Algorithms
대부분의 분할정복 알고리즘은 아래와 같은 구조로 작성된다.
- Divide
- Combine
- Degenerate case
1. Tournament
URG, FRA, BRA, BEL, SWE, ENG, RUS, ERO 8팀이 치르는 토너먼트 경기 알고리즘이다.
- Iterator(
for, while등)방식으로 풀 수도 있지만, 재귀로 작성하면 훨씬 직관적이다.- 함수를 호출하면 s
(시작 index)와e(끝 index)의 중간 인덱스인m을 구한다. - Lwinner에
s부터m까지의 우승자를 구한다. (재귀 호출이다) - Rwinner에는
m+1부터e까지의 우승자를 구한다. (재귀 호출이다) - 최종적으로 Lwinner와 Rwinner 중에서 우승자를 가리고 결과를 반환한다.
- 함수를 호출하면 s
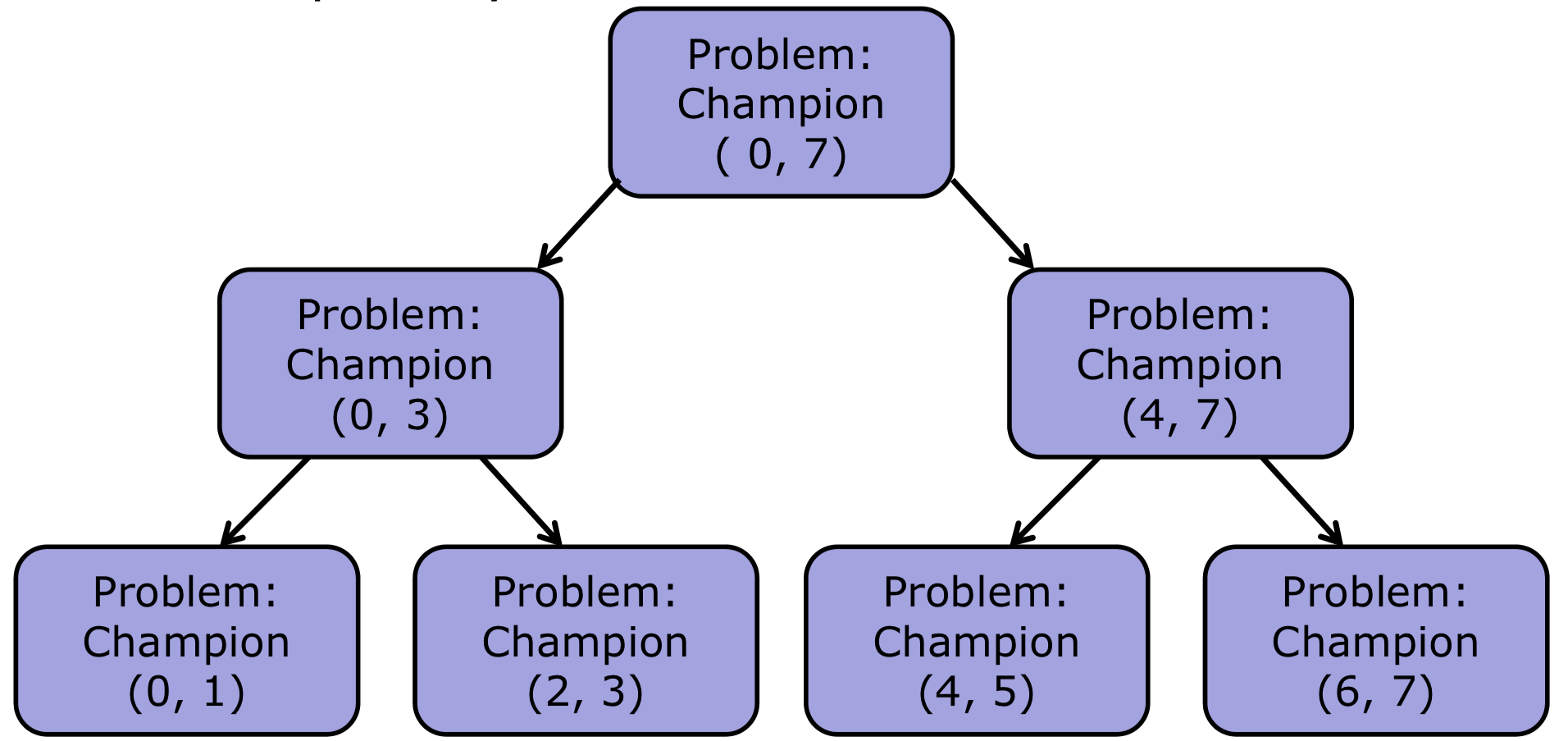
 이해하기 편하게 트리구조를 그려 재귀 동작 방식을 나타낼 수 있다.
이해하기 편하게 트리구조를 그려 재귀 동작 방식을 나타낼 수 있다.
- 각
Champion(0,1)메서드의 실행 순서를 번호로 나타내면 아래처럼 가능하다.
Three Key Points
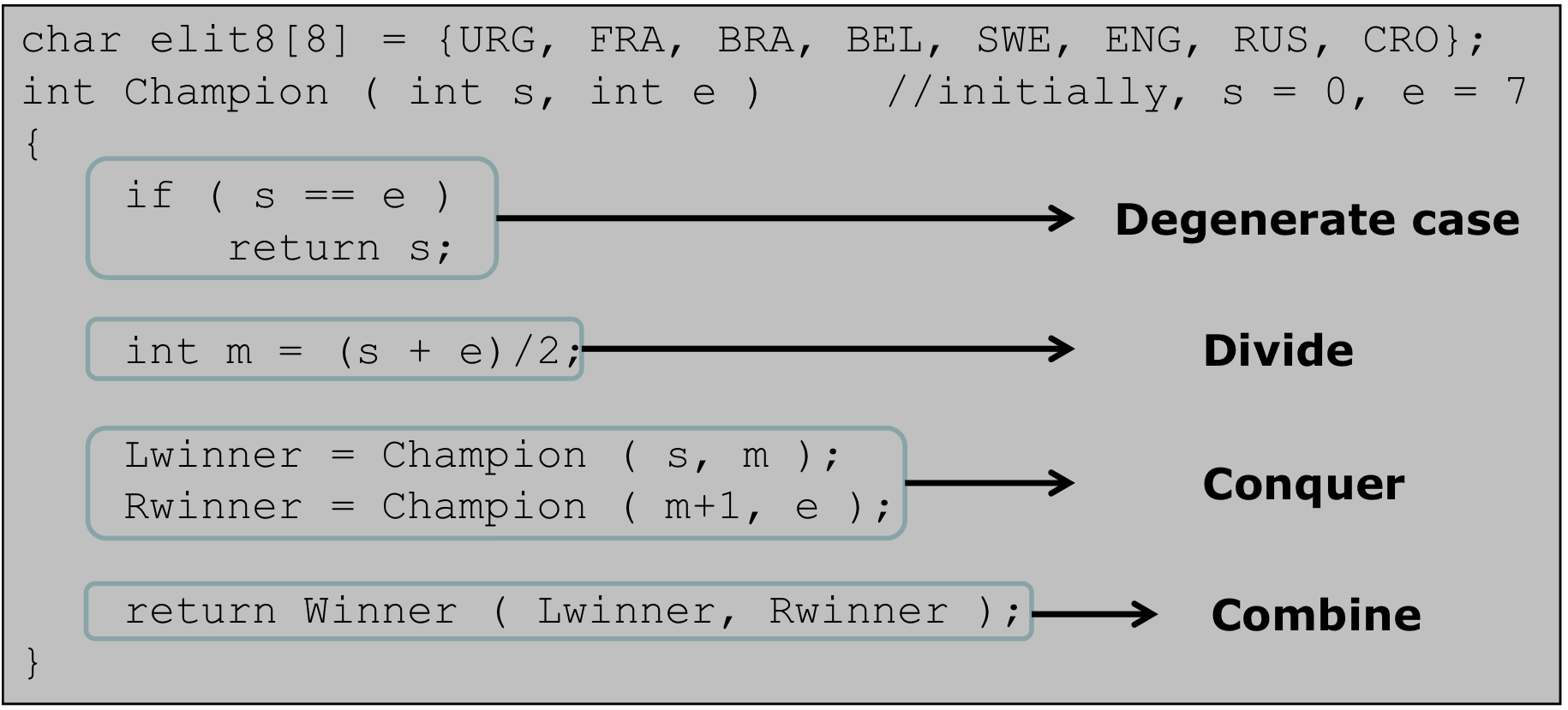
Divide, Conquer, Combine을 알 수있다.- 또한
Degenerate Case를 추가했다.
Three Check Points
- Same format
Champion(Start index, End index)를 매 호출마다 동일하게 호출한다.
- Reduced problem size
- 매
Champion()마다m을 구하기 위해 1/2만큼 나누고s~m, m+1~e로 점점 처리양이 작아진다.
- 매
- Degenerate case
s==e(s==1)일 때 이다.
Time Complexity
토너먼트 알고리즘의 시간복잡도는 다음과 같다.
먼저 Divide & Conquer (분할정복) 알고리즘들은 대부분 마스터 정리의 형태처럼 나타낼 수 있다.
$T(n)=aT(\frac{n}{b})+O(n)^d$
따라서 토너먼트 알고리즘은 다음과 같다.
$T(n)=2T(\frac{n}{2})+O(1)$
- 따라 $0 < log_2 = 1$이므로, 토너먼트 수식 시간복잡도는 $O(n^{log_22}) = O(n)$ 이다.
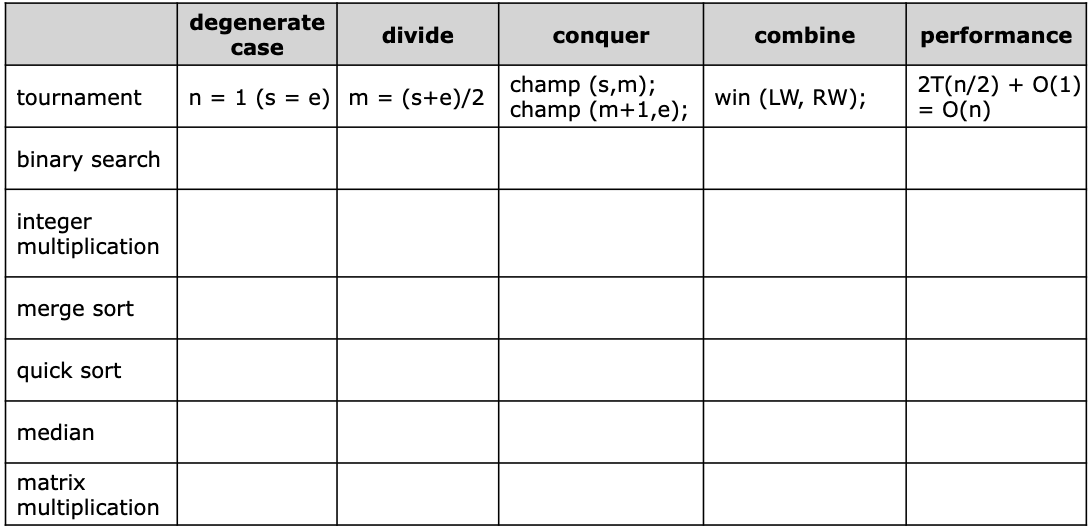
2. Binary Search
이진 탐색은 정렬된 배열에서 중앙 값을 찾고자 하는 값과 비교하며 나아가는 알고리즘이다.

Three Key Points
- Divide
m = (s+e)/2를 에서 중앙 값으로 나누는 것을 확인할 수 있다.
- Conquer
- 중앙 값이 찾고자 하는 값에 따라 구간을 바꿔 값이 존재하는지 확인한다.
- Combine
- 값을 찾았다면 그 값을 반환하면 되기 때문에 Combine이 없다.
Three Check Points
- Same format
- 모든 함수는
binary_search(Start index, End index, find value)형식으로 동일하다.
- 모든 함수는
- Reduced Problem Size
- 중앙 값이 찾고자 하는 값보다 더 클 경우는 시작부터 중앙 인덱스-1만큼 반복해 1/2로 처리양을 줄인다.
- 중앙 값이 찾고자 하는 값보다 더 작은 경우는 중앙 인덱스+1부터 끝까지 반복해 1/2로 처리양을 줄인다.
- Degenerated case
s==e(s==1)일때 이다.
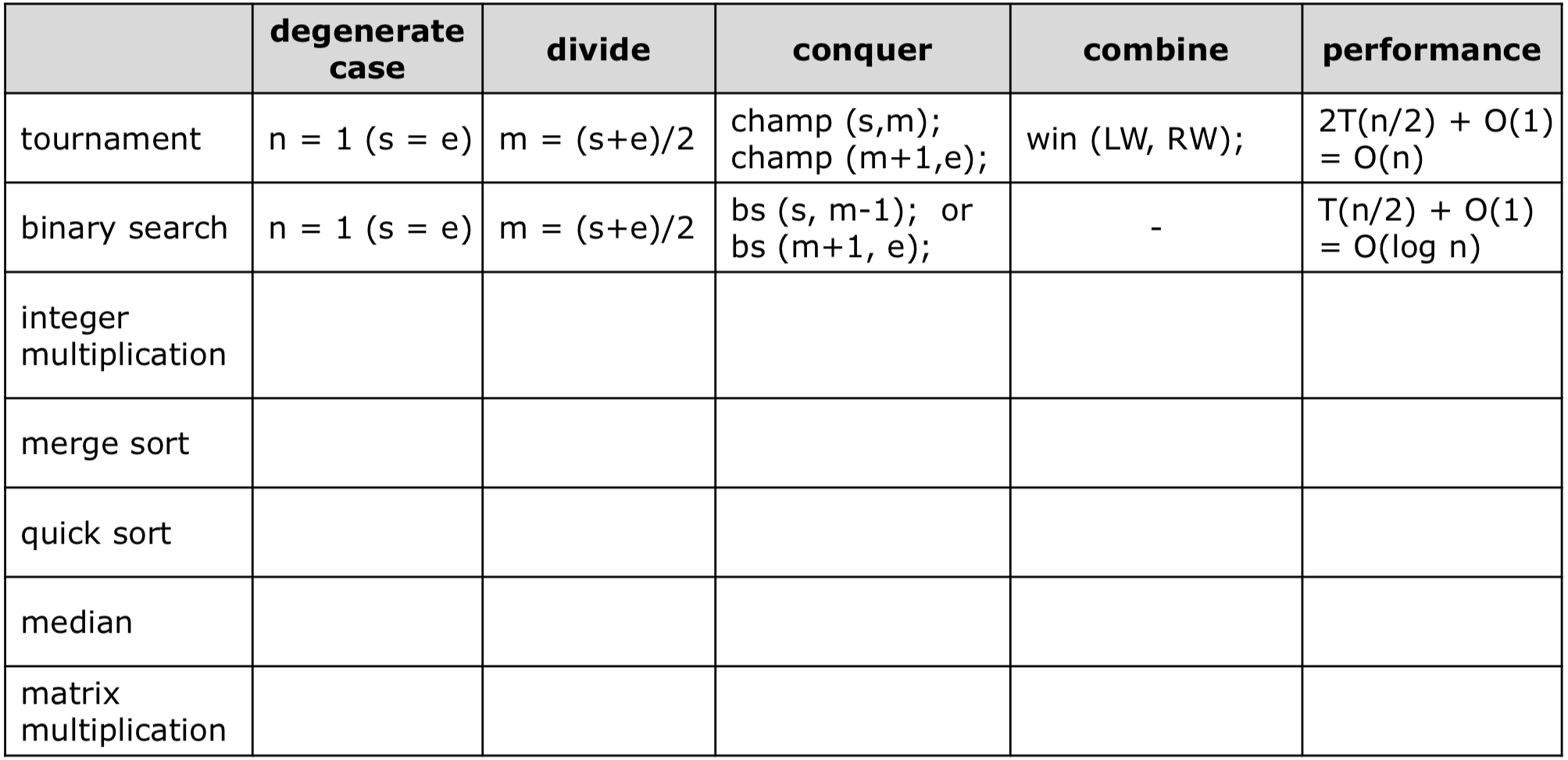
Time Complexity
토너먼트와 다르게 이진 검색은 조건에 따라 한 함수에서 자신을 한번만 호출한다. 또한 이진 검색은 Combine이 없다. 따라서 아래와 같이 표현이 가능하다.
$T(n)=T(\frac{n}{2})+1$
Master theorem 공식을 대입 하면 a==1, b==2, d==0 이므로, $0 = log_21$ 이다. 따라서 $O(1+log\text{ }n)=O(log\text{ }n)$이다.
3. Multiplication
- 이진수의 곱셈은 일반적으로 $O(n^2)$의 시간복잡도를 가진다. 각 자릿수 별로 곱하기 때문이다. 이 방법을 분할 정복을 사용하면 더 빠르게 계산이 가능하다.
- 가우스 정리로 아래와 같이 4번을 곱해야 하는 계산을 3번의 곱으로 해결할 수 있다.
$(a+bi)(c+di)=ac-bd+(ad+bc)i$
$ad+bc=(a+b)(c+b)-ac-bd$
- $ac$와 $bd$의 곱은 이미 위 식에서 계산이 되었기 때문에 $(a+b)(c+b)$의 곱만 한 번 해주면 된다.
- $X=10111111{(2)}$, $Y=10111010{(2)}$ 에서
- → $X=1011{X_L}1111{X_R}$, $Y=1011{Y_L}1010{Y_R(2)}$과 같이 중앙값을 기준으로 $X_R, X_L, Y_R, Y_L$을 구한다.
- $X=[X_L][X_R]=2^SX_L+X_R$
- $Y=[Y_L][Y_R]=2^SY_L+Y_R$ where $s=\frac{n}{2}$ 두 식을 곱하면
- $XY=(2^SX_L+X_R)(2^SY_L+Y_R)$ $=2^nX_LY_L+2^S(X_LY_R+X_RY_L)+X_RY_R$ 로 풀 수 있다.
- 위 식의 시간복잡도를 나타내면 $T(n)=4T(2/n)+O(n)$으로 나타내진다.
- 위 식의 시간복잡도는 $O(n^2)$로 아무런 개선이 없는 상태다.
- 여기서 가우스의 아이디어를 적용하면 아래와 같이 시간복잡도를 낮출 수 있다.
- $X_LY_R+X_RY_L=(X_L+X_R)(Y_L+Y_R)-X_LY_L-X_RY_R$
- → $T(n)=3T(2/n)+O(n)$
- 위 식을 Master Theorem으로 풀어보면 $O(n^{log_2^3})$으로 약 $O(n^{1.7})$이다.
- 위 공식을 코드로 나타내면 아래와 같다.
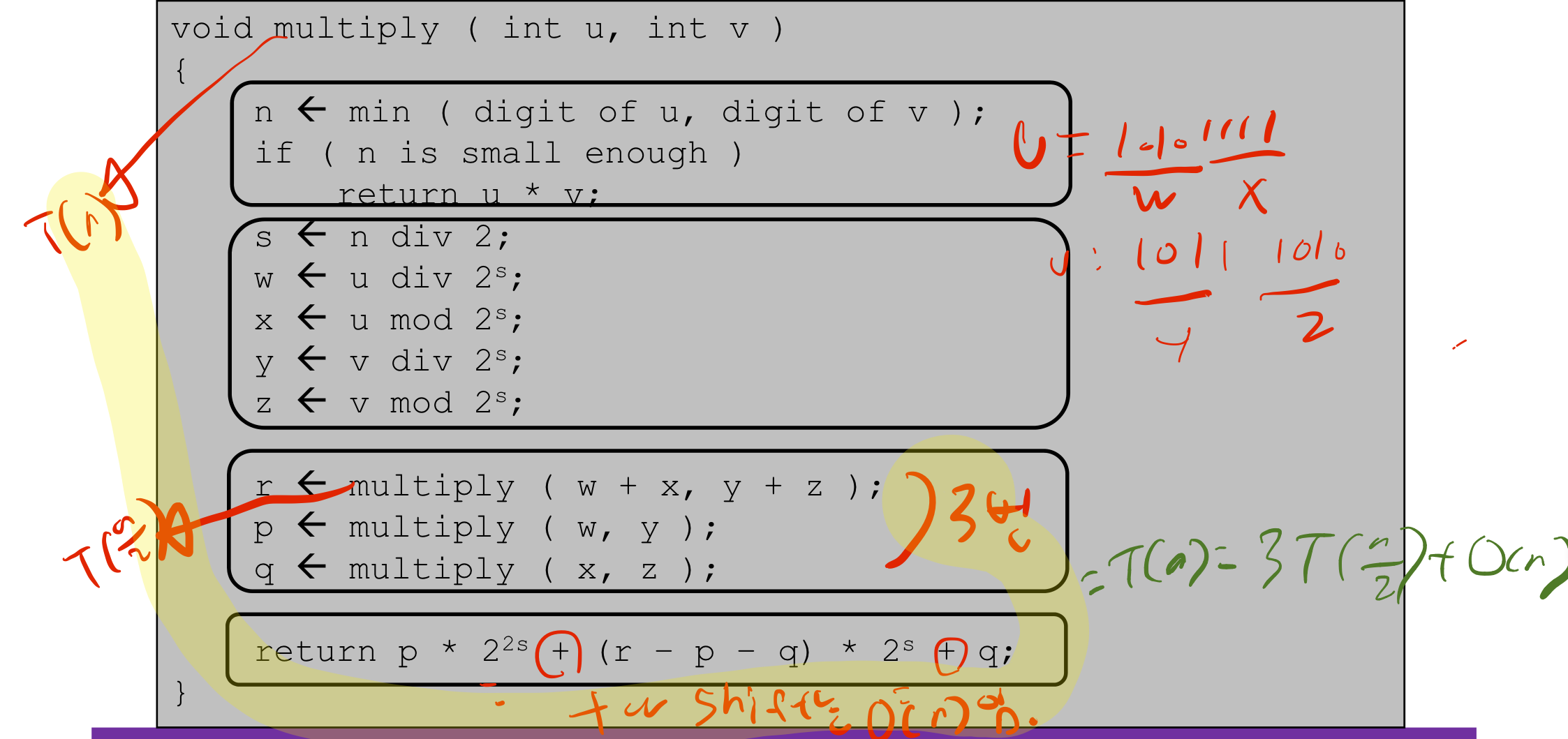
Three Key Points
- Divide
s, w, x, y, z을 각각div 2와mod 2로 나눈다.
- Conquer
r, p, q에 각각multiply()를 호출해 계산한다.multiply()를 총 3번 호출한다.
- Combine
- 결과를 $+$와 Shift로 combine해 반환한다.
- $+$와 Shift는 O(n)번 소요된다.
- 결과를 $+$와 Shift로 combine해 반환한다.
Three Check Points
- Same format
- 계산하고 곱셈할 u와 v를 매번 공통으로 받는다.
- Reduced Problem Size
- 2로 나눈 값과 나머지를 이용해 함으로 점점 값이 작아진다.
- Degenerated case
- n이 적절히 작아졌다면 반환한다.
Time Complexity
multiply()는 매 함수 실행마다 3번 자신을 호출하고, 2로 나눈 값과 나머지를 사용해 계산한다.- 따라서 Multiplication의 시간복잡도는 다음과 같다.
$T(n)=3T(2/n)+O(n)$
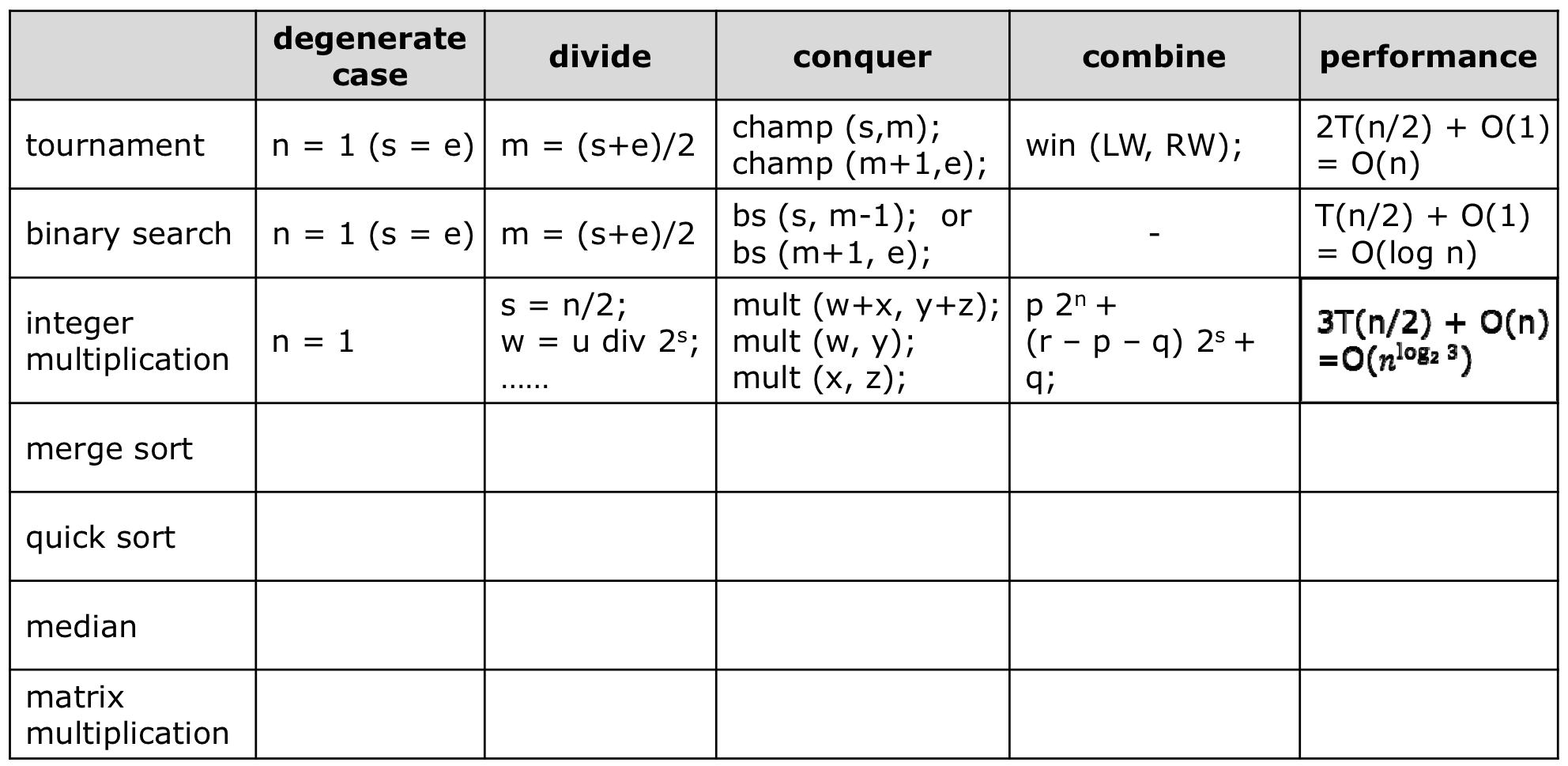
4. Merge Sort
합병 정렬은 1945~1946년 즈음 폰 노이만이 제시한 정렬 알고리즘이다. 배열을 반으로 쪼개 각 집합을 정렬하고 정렬된 집합을 합치는 것이다.

- merge 코드

- 실행 순서는 다음과 같다.
merge()함수는A[]배열의 부분 배열ls~le와rs~re를 합병하여 정렬된 배열을 생성하며, 동시에 복사할 배열B[]의 포인터를 다루어 Three Pointer Algorithm을 활용한다.- 합병 결과는 두 정렬된 부분 배열을 합쳐 완전히 정렬된 배열이다.
-
while문에서lptr과rptr이 각 부분 배열의 끝을 넘어가지 않을 때까지 반복한다.a.
lptr과rptr값을 비교하여 작은 값을B배열의bptr에 넣는다.b. 값이 넣어진 포인터를 오른쪽으로 이동시킨다.
while문 종료 후, 남은 부분 배열의 원소들을B배열에 복사한다.- 이로써
B[]에는 정렬된 배열이 생성되며 함수가 종료된다.
- 각 번호는 코드의 실행 순서이다.
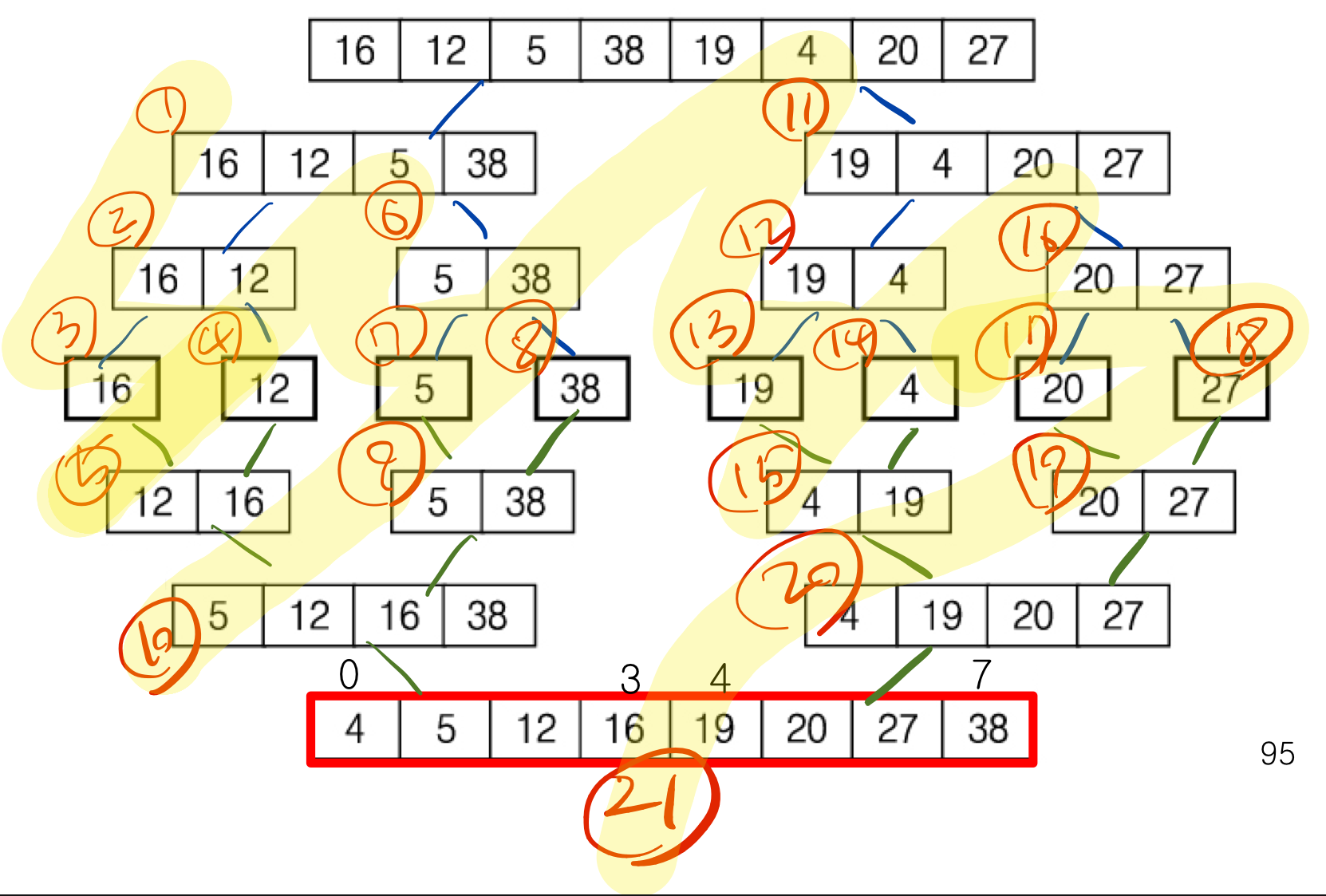
Three Key Points
- Divide
- 매번 m에 배열의 중앙 값을 기준으로 나눈다.
- Conquer
- 중앙 값 기준 왼쪽과 오른쪽으로 2번 정렬을 진행한다.
- Combine
- 정렬된 두 배열을
merge()메서드를 통해 combine한다.
- 정렬된 두 배열을
Three Check Points
- Same format
- 항상 시작 인덱스, 끝 인덱스, 배열을 입력받는다.
- Reduced Problem Size
- 중앙 값 기준으로 나눠 처리양이 점점 감소한다.
- Degenerated case
s==e(s==1)일 때이다.
Time Complexity
- 합병 정렬은 매번 $1/2$로 나눠서 왼쪽, 오른쪽 배열 정렬로 두 번씩 자신을 호출한다. 그리고 combine에는 $O(n)$만큼 걸린다.
$T(n)=2T(\frac{n}{2})+O(n)$
- 위 식을 빅오 표기법으로 풀어보면
a=2,b=2,d=1으로 $1 = log_22 = O(n^{log_22}\text{ }log\text{ }n)=O(n\text{ }log\text{ }n)$이다.
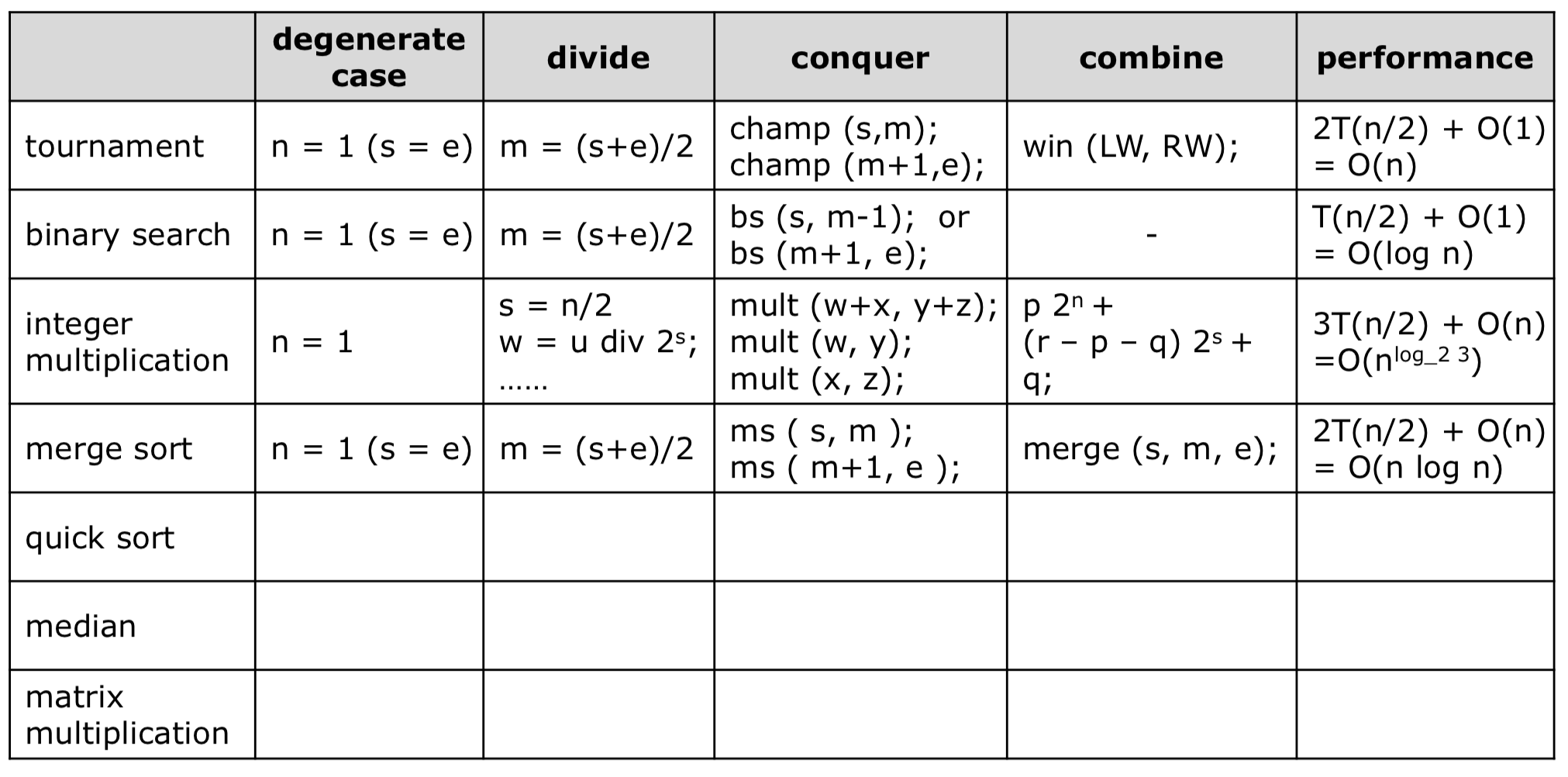
5. Quick Sort
- 퀵 정렬은 합병 정렬을 개선한 알고리즘으로, 평균에서 더 좋은 성능을 내며, binary search와 같이 combine 단계가 없는 특이한 알고리즘이다.
- 합병 정렬은 배열의 중앙 값을 기준으로 좌/우 를 나눠 정렬한 것이라면, 퀵 정렬은 한 피봇을 중심으로 왼쪽은 피봇보다 작은 값, 오른쪽은 피봇보다 큰 값으로 정렬해 나가는 기법이다.
- 처음 정렬될 때 피봇 기준 좌/우만 나누니 정렬의 순서는 상관이 없다. 즉, 퀵 정렬은 이 피봇(pivot) 값을 찾아내는 것이 핵심이다.
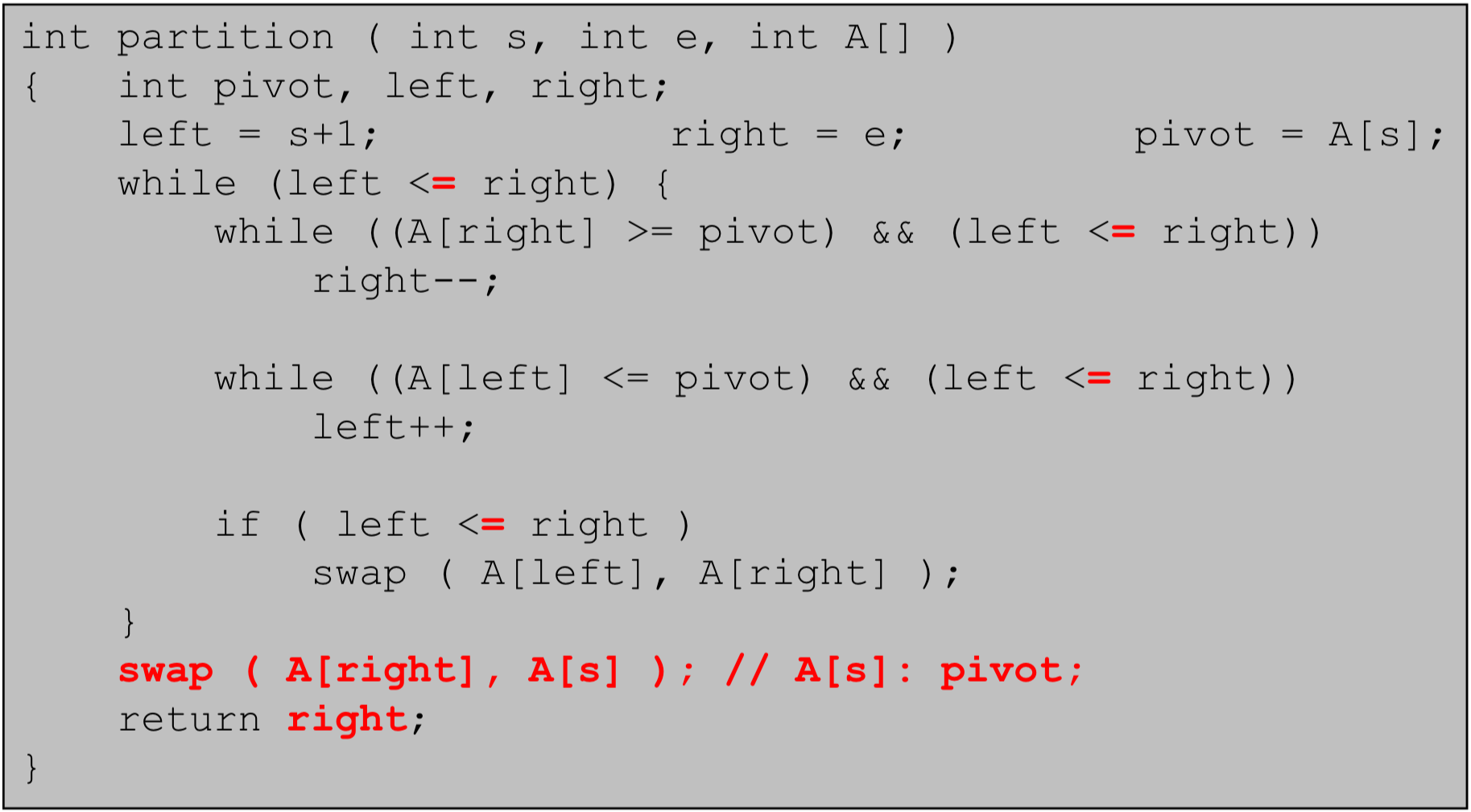

quickSort()함수는 퀵 소트(Quick Sort) 알고리즘을 사용하여 배열을 정렬하는 함수이다.- 퀵 소트는 분할 정복(divide and conquer) 방식을 사용하여 배열을 정렬한다. 주어진 배열을 기준(pivot)을 사용하여 두 개의 부분 배열로 나눈 후 각 부분 배열을 재귀적으로 정렬한다.
-
함수의 핵심은
partition()함수로, 이 함수에서는 배열을 기준을 중심으로 왼쪽은 작은 값들, 오른쪽은 큰 값들로 분할한다.a.
pivot을 기준으로 작은 값은 왼쪽에 큰 값은 오른쪽에 정렬한다.b.
pivot의 최종 위치를 반환한다. -
quickSort()함수에서는 분할된 두 부분 배열을 각각 재귀적으로 정렬한다.a. 왼쪽 부분 배열에 대해
quickSort()를 호출한다.b. 오른쪽 부분 배열에 대해
quickSort()를 호출한다. - 재귀 호출을 통해 모든 부분 배열이 정렬된 후, 배열 전체가 정렬된다.
- 함수가 종료되면 배열은 정렬된 상태로 남게 된다.
Three Key Points
- Division
partition()을 통해pivot값을 구한다.- 즉, 배열을 좌/우 측으로 분할한 것이다.
- 또한, partition이 실행되면 합병 정렬과 달리
pivot보다 작은 값, 큰 값으로 정렬된다. 이에 combine단계를 없앨 수 있다.
- Conquer
pivot기준 좌/우측에 퀵 정렬을 진행한다.
- Combine
- 퀵 정렬에는 combine단계가 없다.
Three Check Points
- Same format
- 시작 인덱스, 끝 인덱스, 정렬할 배열을 동일하게 받는다.
- Reduced problem size
pivot기준으로 나눠지기 때문에 처리양은 감소한다.
- Degenerate case
s가e보다 작아질 경우이다.- 합병 정렬과 다르게
s가e보다 커질 수 있기 때문이다.
- 합병 정렬과 다르게
Time Complexity
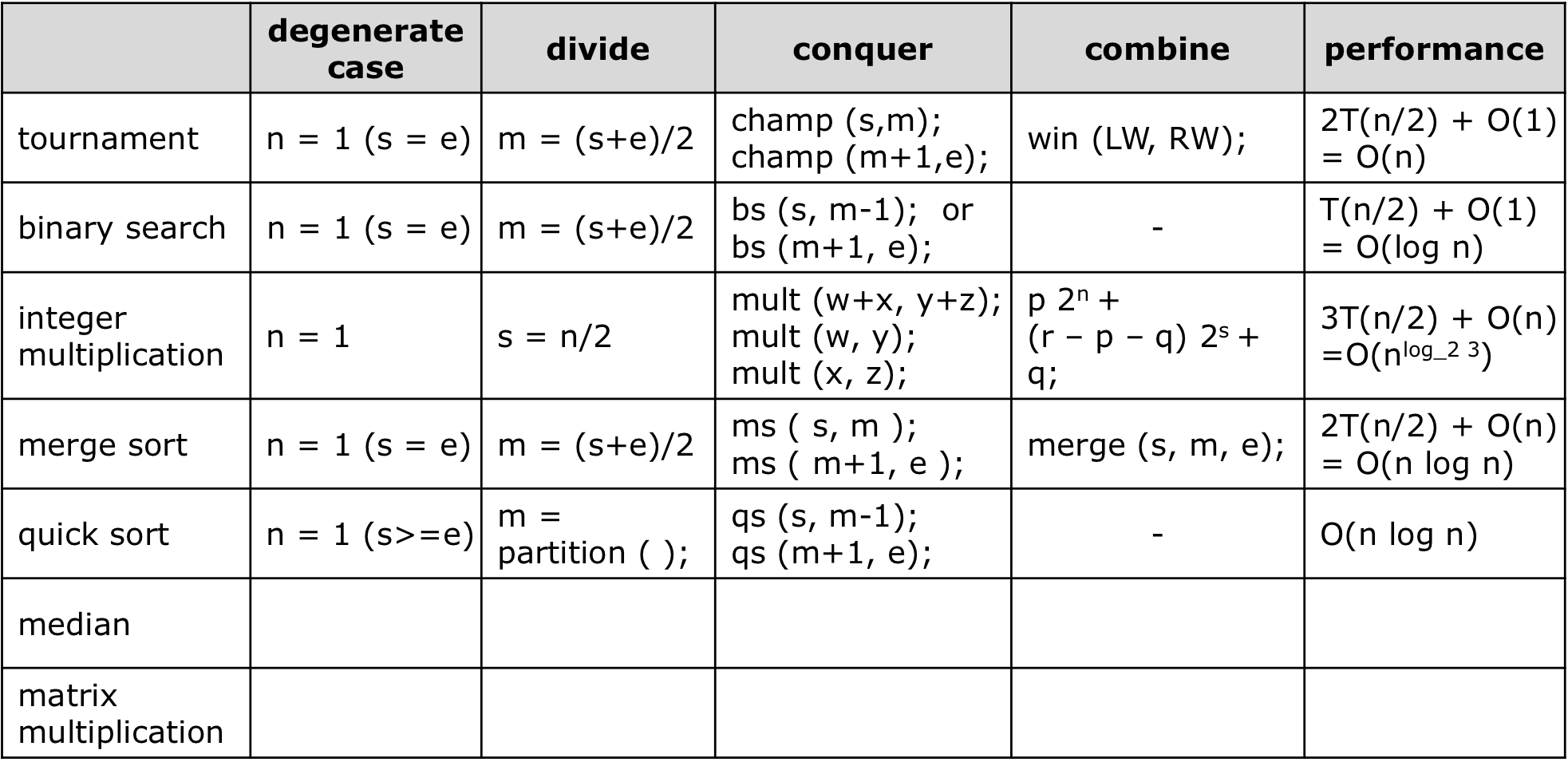
퀵 정렬의 case별 성능표이다.

- Best case
- 항상
pivot이 배열의 중앙에 있을 때다. - $T(n)=2T(\frac{n}{2})+O(n) = O(n\text{ }log\text{ }n)$이다.
- 항상
- Average Case
- 평범하게 정렬되어 있는 배열이다.
- $T(n)=\frac{1}{n}\sum_{k=1}^n(T(k-1)+(n-k)+O(n) = O(n\text{ }log\text{ }n)$이다.
- Worst case
- 역순으로 정렬되어 있는 배열이다.
- $T(n)=T(n-1)+O(n)=O(n^2)$ 이다.
6. Median
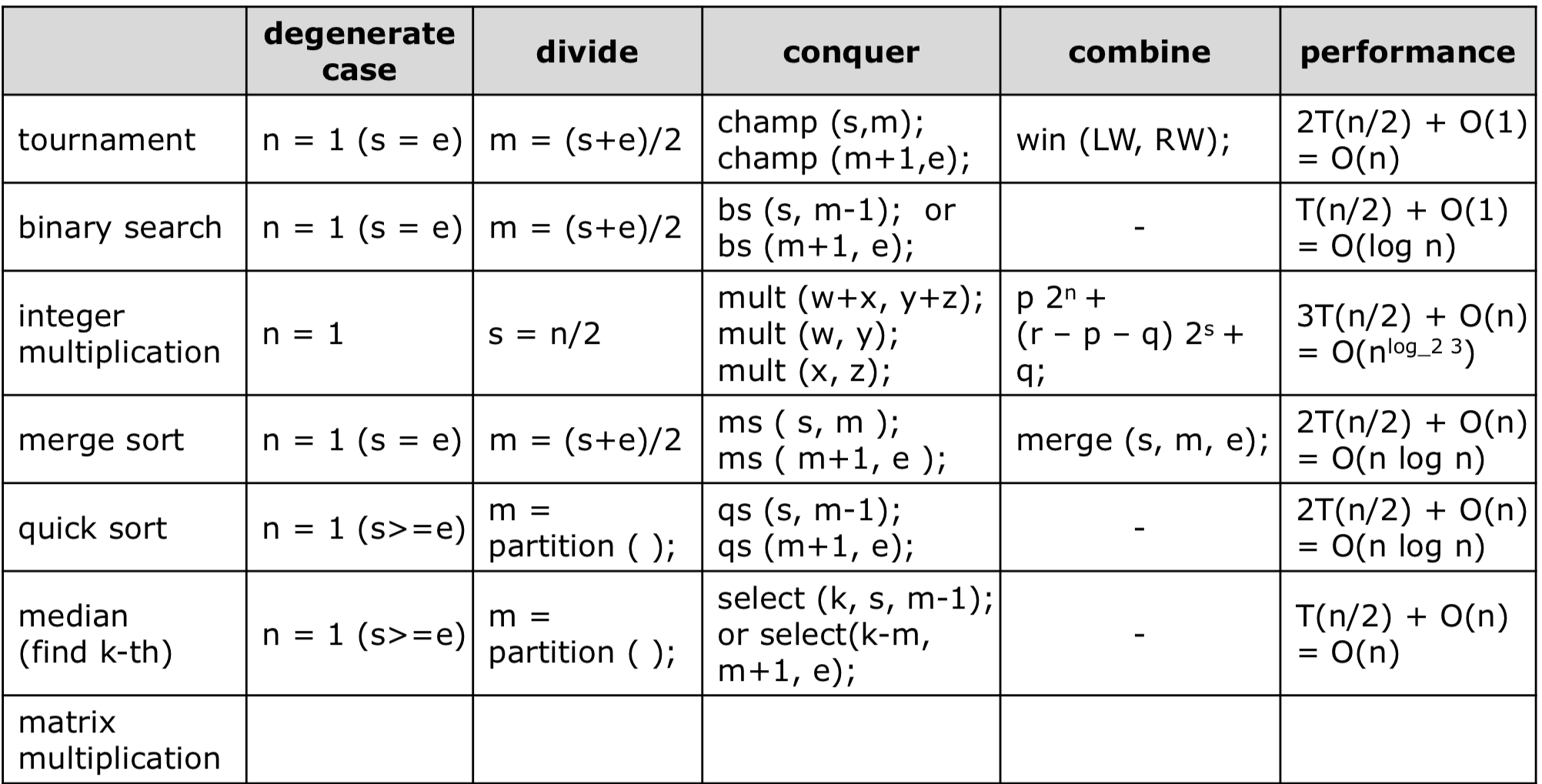
Median은 배열의 중앙 값을 찾는 알고리즘이다.
[20, 1, 10, 30, 25]라는 배열에서 중앙 값은20이다. 이를 퀵 정렬의 partition을 통해 구할 수 있다.

- 먼저 partition을 통해 m을 구한다.
- 만약 찾고자 하는 값이 m과 같다면 그 값을 반환한다.
- 만약 찾고자 하는 값이 m보다 작다면 왼쪽에 대해서 재귀를 실행한다.
- 만약 찾고자 하는 값이 m보다 크다면 오른쪽에 대해서 재귀를 실행한다.
Three Key Points
- Divide
- partition을 통해 나눈다.
- Conquer
- k와 m의 값을 비교해 좌/우로 나눠 k번째를 찾는다.
- Combine
- combine은 없다.
Three Check Points
- Same format
- 찾고자 하는 k번째 수, 시작 값, 끝 값으로 동일하다.
- Reduced problem size
- partition한 결과의 좌/우를 실행해 처리양은 감소한다.
- Degenerate case
- s==e(s==1)일 때 이다.
Time Complexity
Median은 divide에 $n$의 시간을 사용하고, conquer에 $\frac{n}{2}$을 사용한다.
즉, $T(n)=T(\frac{n}{2})+O(n)=O(n)$의 시간복잡도를 가진다.
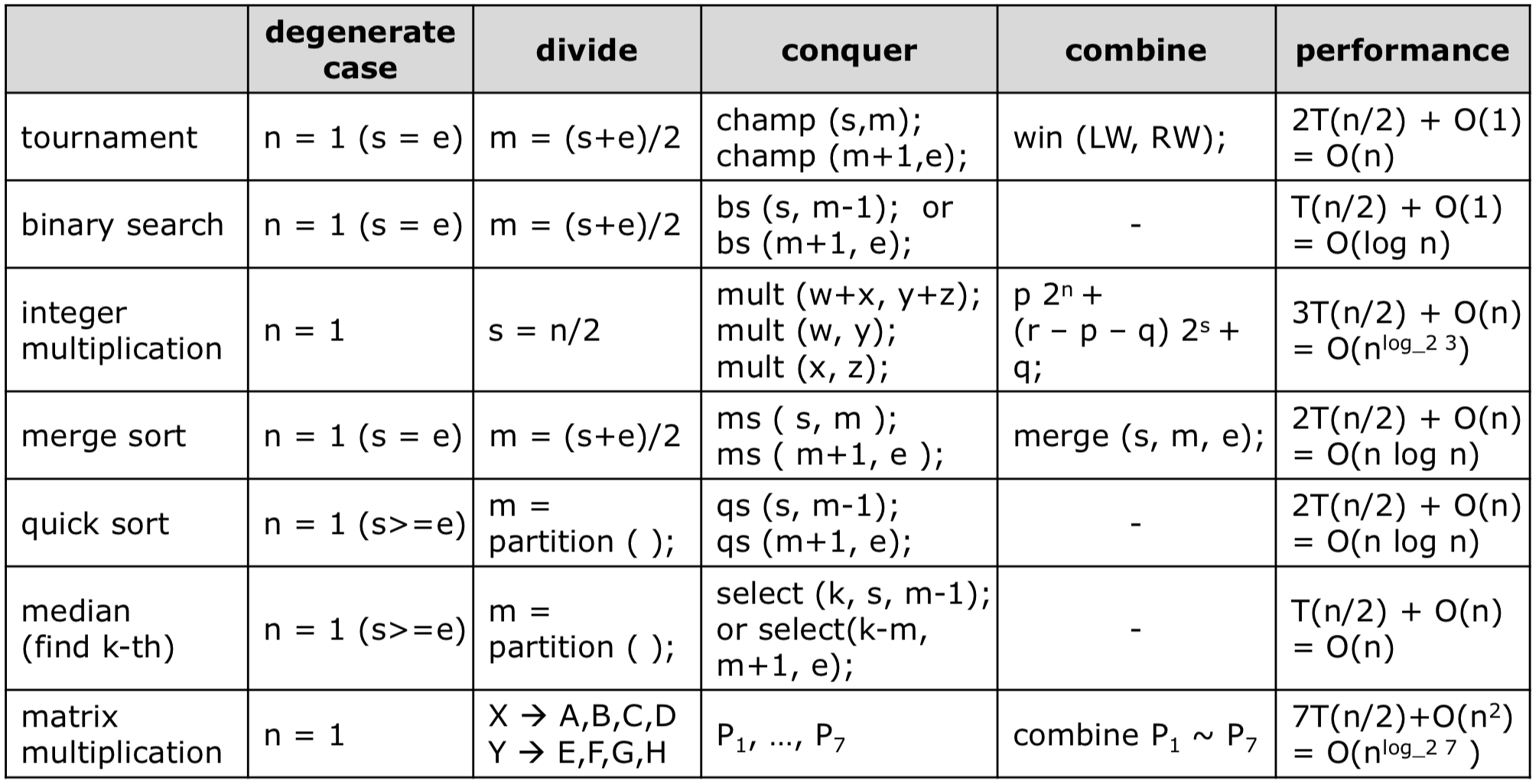
7. Matrix Multiplication
행렬의 곱은 bruteforce 방법으로 $O(n^3)$의 시간복잡도를 가진다. 이에 분할정복을 사용해 조금이라도 시간복잡도를 개선할 수 있다.

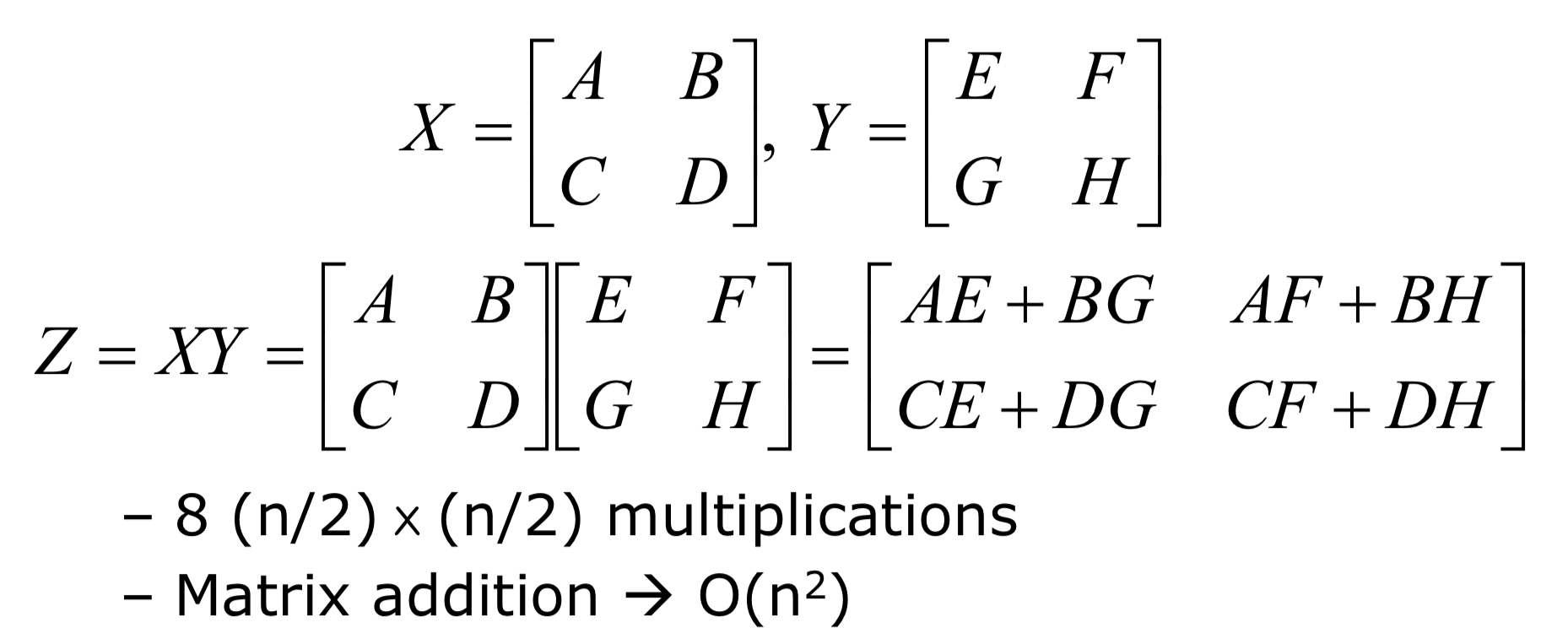
사진과 같이 두 행렬 $X$와 $Y$의 곱을 $8 * (\frac{n}{2}) * (\frac{n}{2})$로 나눠 계산한다.
- 행렬의 합은 $O(n^2)$이 걸린다.
하지만 분할한 행렬의 곱의 시간복잡도를 구해보면 여전히 $O(n^3)$이다.
$T(n)=8T(\frac{n}{2})+O(n^2)$
위 식을 Master theorem으로 풀어보면 a=8,b=2,d=2 로 $2<log_28=n^{log_23}=O(n^3)$이다.
하지만 아래 공식을 통해 해결하면 8번에서 7번의 곱셈으로 바꿀 수 있다.
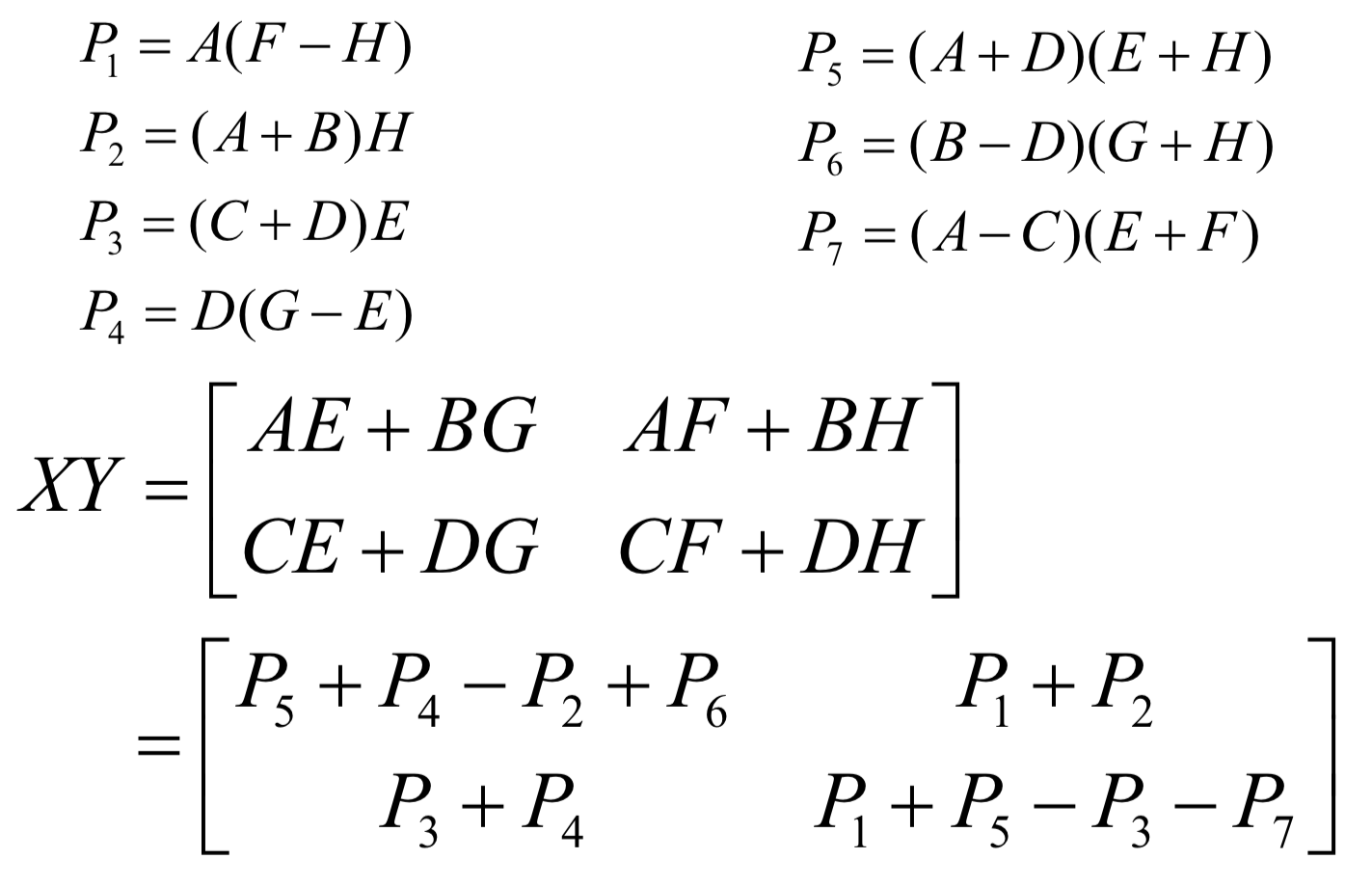
- 기존엔 $AE, BG, AF, BH, CE, DG, CF, DH$로 총 8번 곱해야 하는 계산을
- $P_1$~$P_7$을 이용하면 7번의 곱과 덧/뺄셈으로 해결할 수 있다.
- 이 역시 가우스의 접근방식을 통해 해결한 거라 한다.
개선한 방식의 시간복잡도를 구해보면 다음과 같다.
$T(n)=7T(\frac{n}{2})+O(n^2)$
위 식을 Master theorem으로 풀어보면 a=7,b=2,d=2 로 $2 < log_27 = n^{log_27}=O(n^{2.81})$ 이다.
Three Key Points
- Divide
- $X$를 $A, B, C, D$로, $Y$를 $E, F, G, H$로 분할했다.
- Conquer
- $P_1…P_7$의 곱을 통해 계산한다.
- Combine
- $P_1…P_7$의 결과를 아래 공식처럼 계산한다.
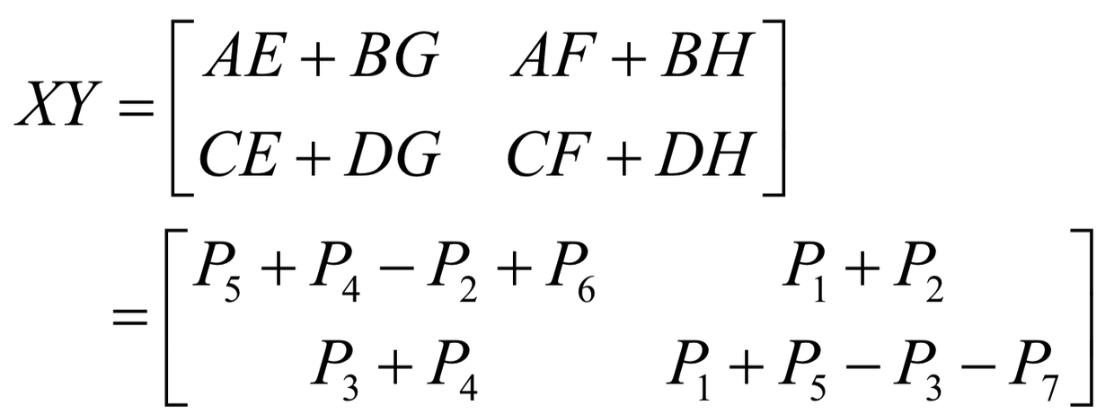
댓글남기기