[알고리즘으로 단단해지기] 4.그래프 BCC (Biconnected graph)
BCC (Biconnected graph)
BCC는 둘 이상의 정점들이 모두 연결되어 있는 그래프이다.
SCC는 directed graph일 때 사용하지만, BCC는 undirected graph일 때 사용할 수 있다.
분절점 (Articulation point)
분절점이란 무방향 그래프 (undirected graph)에서 한 정점을 삭제 했을 때 그래프가 2개 이상으로 나누어지는 정점을 의미한다.
- 2를 삭제한다면 그래프가 2개로 나뉜다.
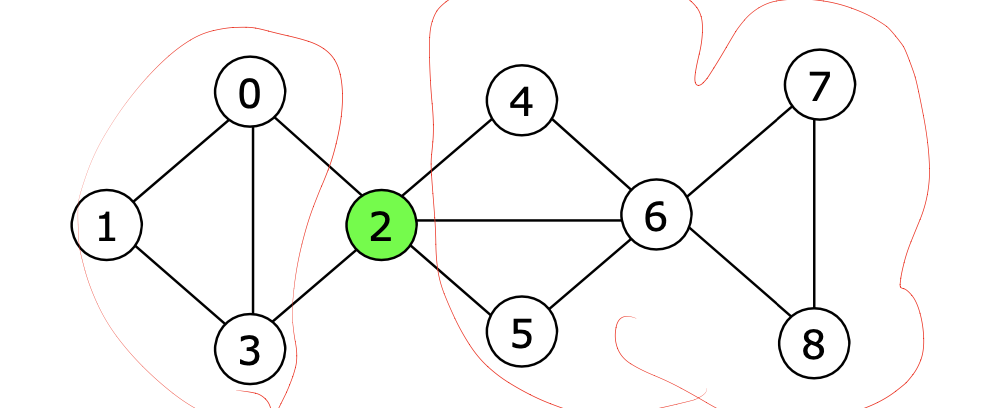
- 6을 삭제하면 그래프가 2개로 나뉜다.
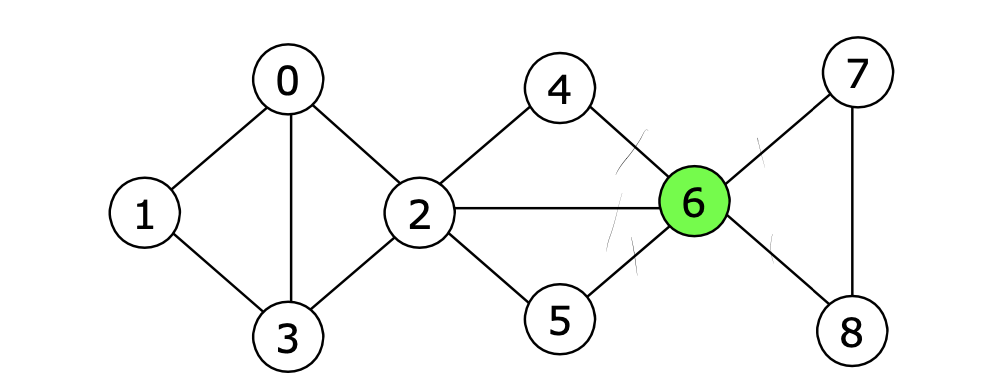
이처럼 한 정점을 삭제했을 때 그래프가 둘 이상으로 나뉜다면, 그 정점을 분절점 (Articulation Point) 이라 한다.
dfn (Depth-first number)
BCC에서는 dfn(depth-first number) 을 통해 분절점을 구할 수 있다.
- dfn은
dfs()를 돌렸을 때 지나는 vertex마다 숫자를 부여하는 것이다.
Depth-First Search (DFS)를 통해 그래프를 탐색할 때, 각 vertex에 대해 dfn 값을 부여하는 것은 그 vertex가 처음으로 발견된(discovered) 시간을 나타낸다. 이 값은 그래프를 탐색하는 동안 순서대로 증가하며 할당된다.
예를 들어, 다음과 같은 그래프가 있다고 가정해보자.
1 --- 2 --- 3
| |
4 --- 5
DFS를 수행하면서 각 vertex에 dfn 값을 할당하는 순서를 살펴보자.
- 시작 (예: 1):
dfn: 1 (처음 발견된 시간)
- 인접한 vertex로 이동 (예: 2):
dfn: 2
- 다시 인접한 vertex로 이동 (예: 3):
dfn: 3
- 다시 이전 vertex로 돌아와서 다른 방향으로 이동 (예: 4):
dfn: 4
- 인접한 vertex로 이동 (예: 5):
dfn: 5
아래 그래프에서 $3$을 root vertex로 잡고, 시작을 $4$번 vertex로 생각하고 dfs를 하면 다음과 같다.
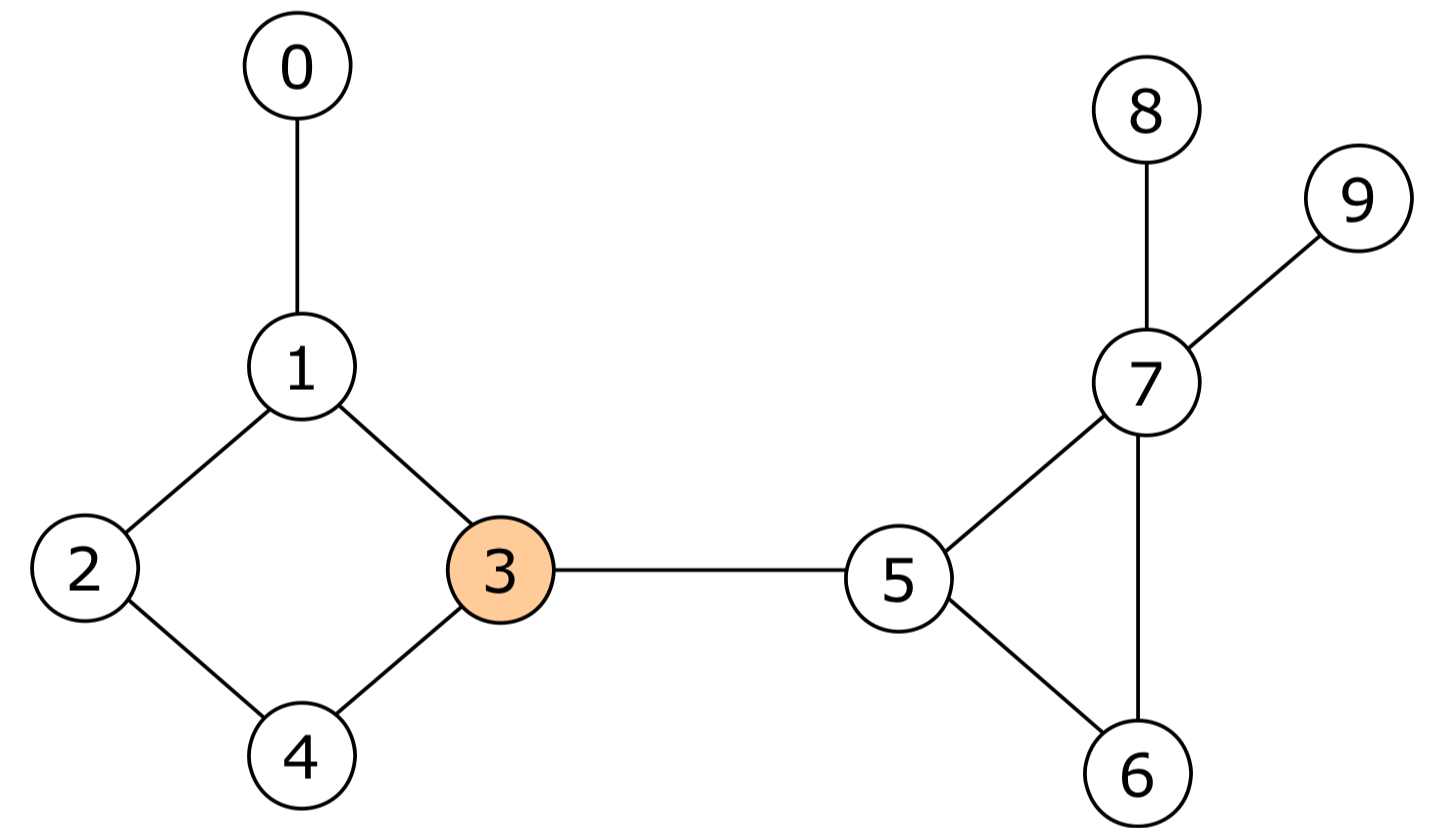
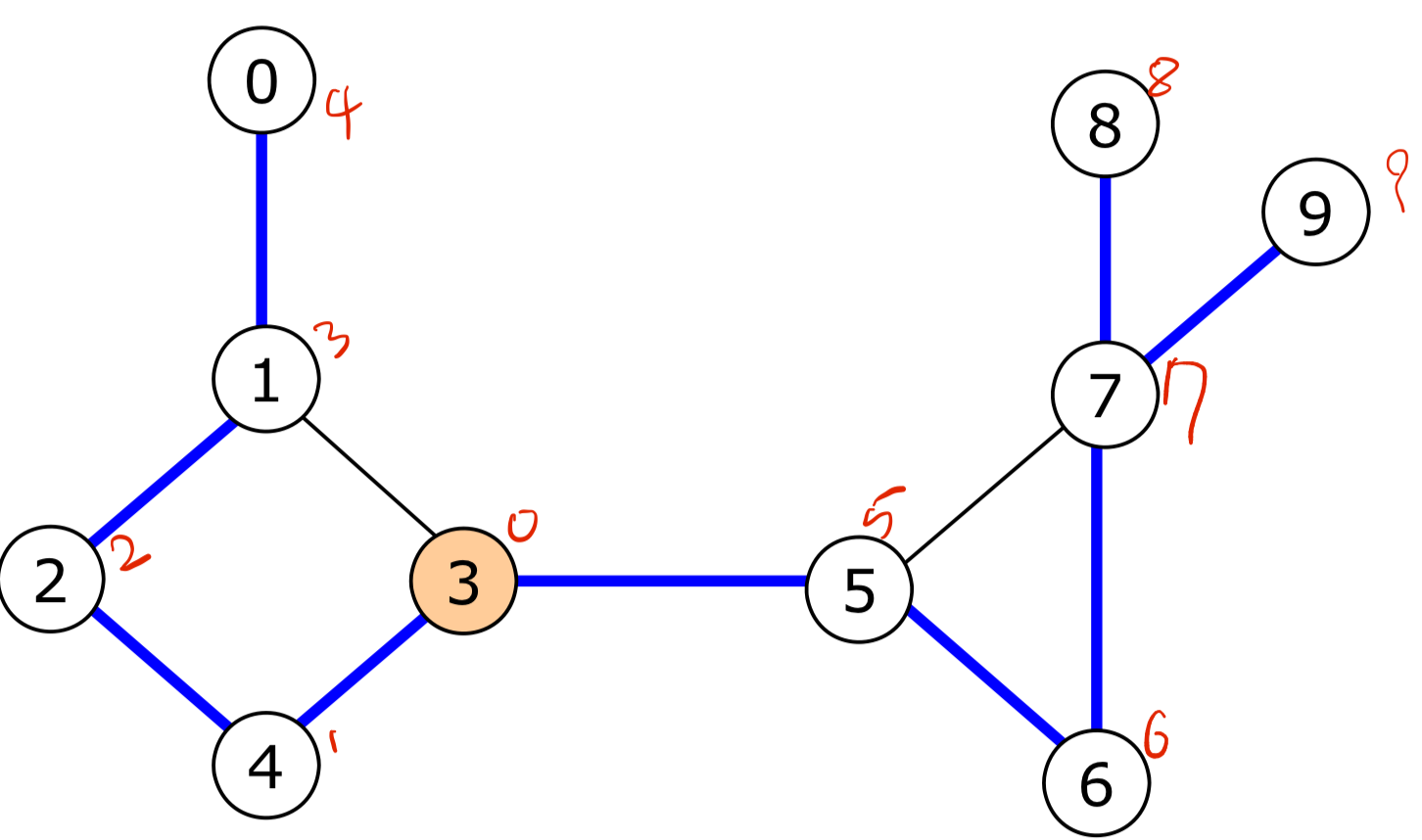
- Spanning Tree 형태로 dfn을 구하면 다음과 같다.
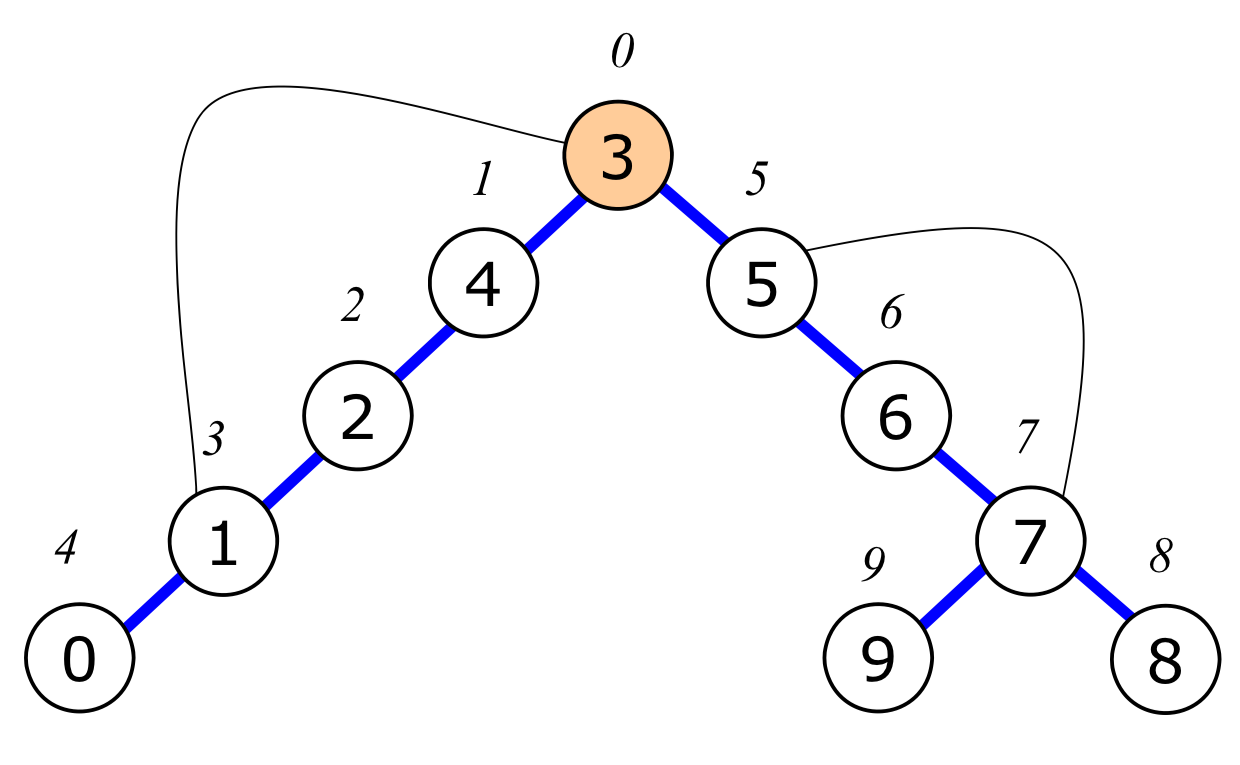
- 위 트리에서 확인할 수 있는 특징은 다음과 같다.
root node에서leaf node로 가는 경로는ancestor↔descendant(조상 ↔ 후손) 관계이다.- 모든
descendant의dfn은ancestor의dfn보다 크다.- $1$ vertex의
dfn은 모든ancestor의dfn보다 크다. - $3$ vertex의
dfn은 모든descendant의dfn보다 작다.
- $1$ vertex의
- 모든
Back Edge
BCC에서의 non-tree edge는 전부 back edge 이다.
-
Undirected graph에서의 edge 종류는 다음과 같다.
- Tree Edge
- Backend Edge
-
아래 그래프와 트리에서
Back Edges부분은 다음과 같다.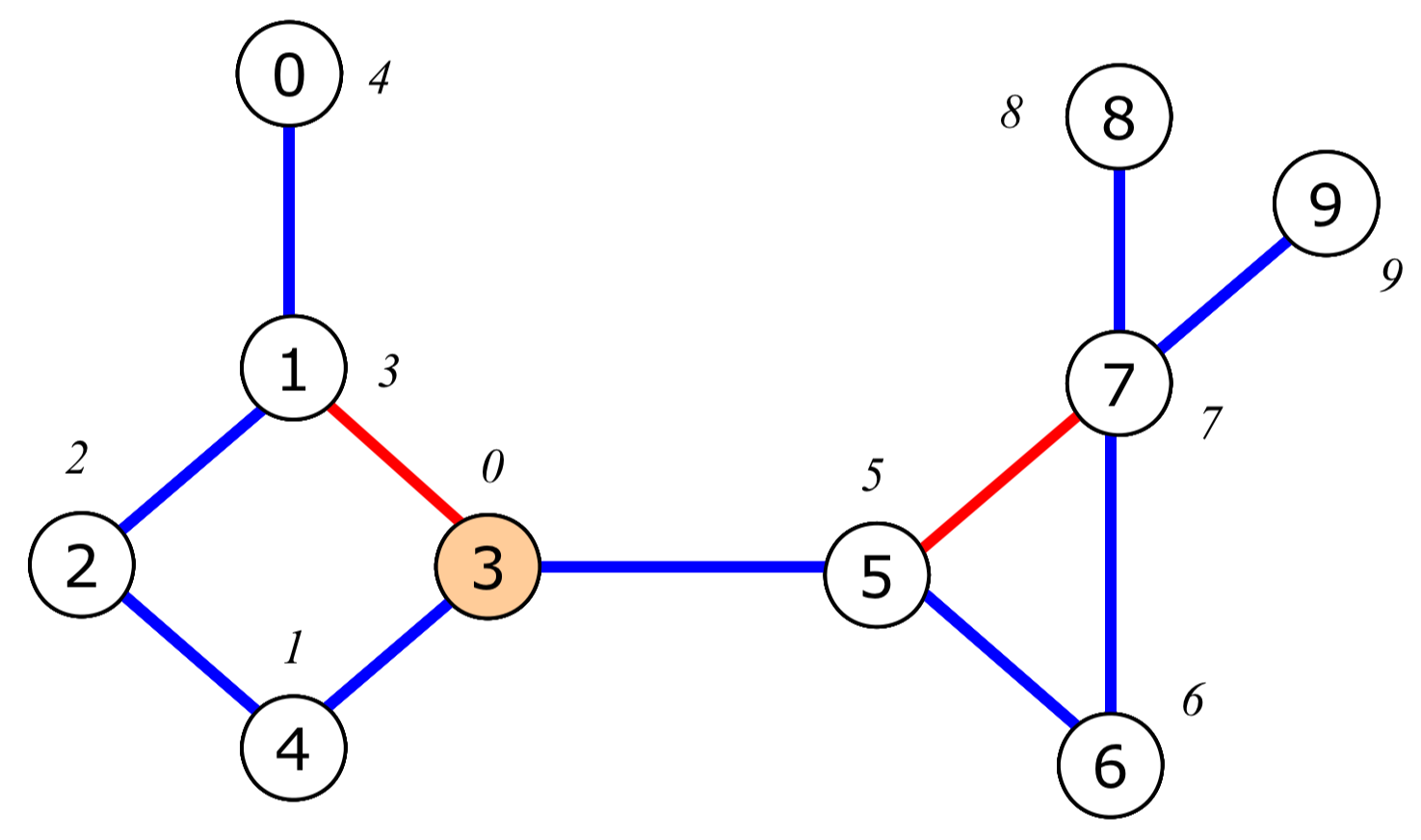
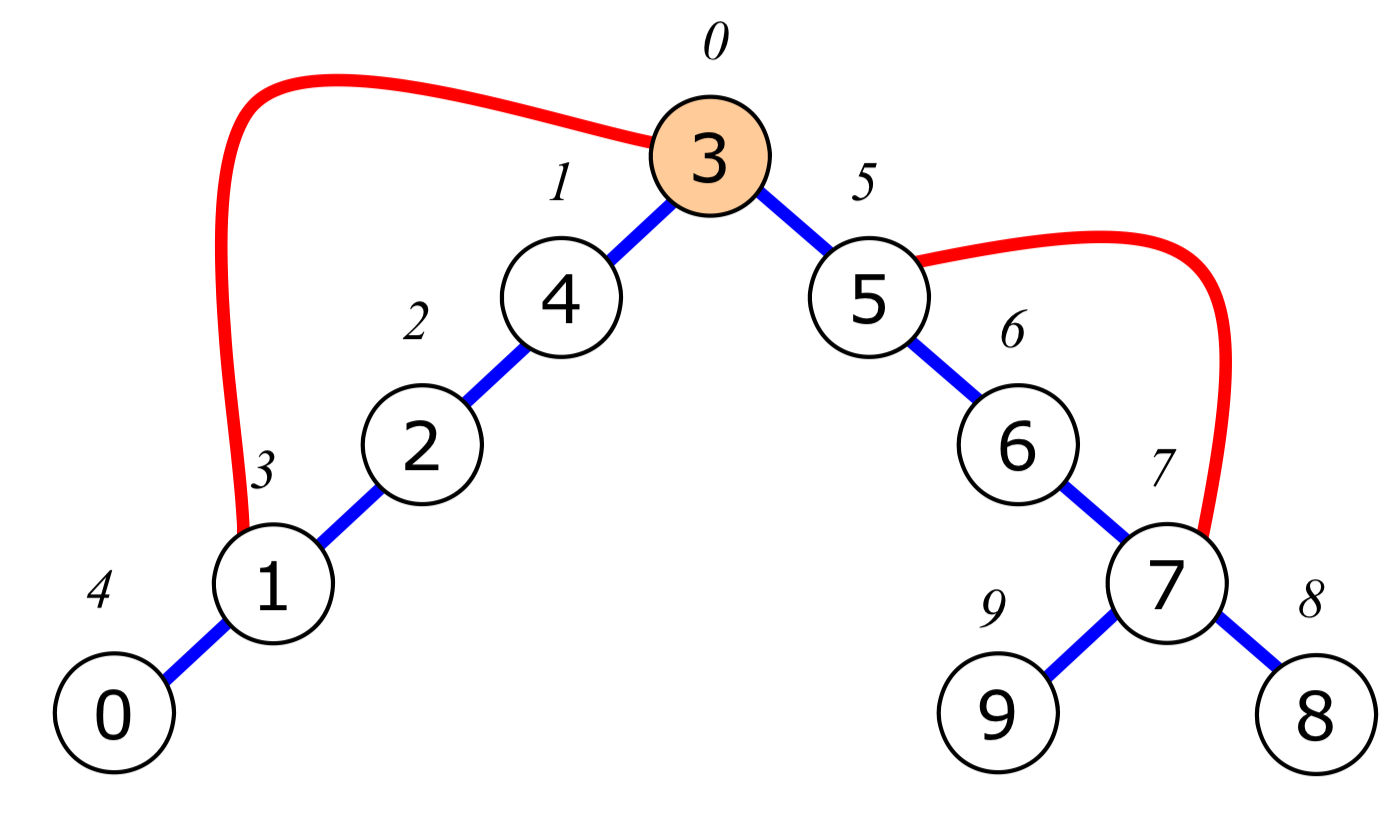
-
이 Back edge를 활용하면 분절점을 쉽게 구할 수 있는데 분절점의 특성은 다음과 같다.
- 한 vertex를 삭제했을 때 두 개의 그래프로 분할되어야 한다.
-
depth-first spanning tree에서 분절점을 찾는 방법은 두 가지가 있다.
-
두 개 이상의 child vertex를 가진다면 분절점이다.
-
즉, 위 tree에서 root node는 분절점이다.
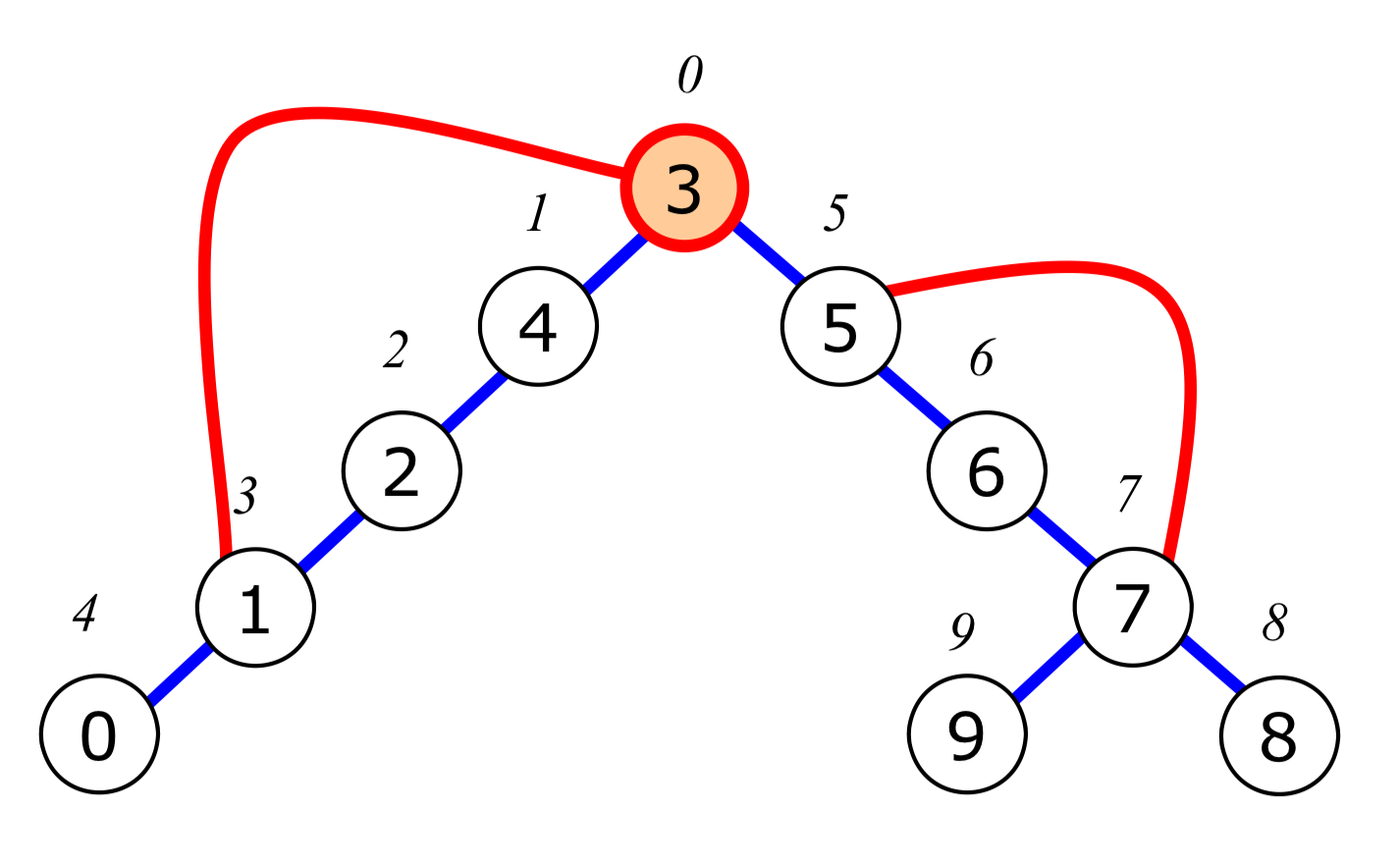
-
-
low() 를 이용하여 구하는 것이다.
-
low()
$low(u)$ 우리는 결국 vertex $u$가 도달할 수 있는 가장 작은 dfn을 구해야 한다.
-
$low(u)$
-
vertex $u$가 자신이 가장 낮은 dfn수로 가기 위한 방법은 3가지 중 가장 작은 값을 구하면 된다.
-
$dfn(u)$
- 자신의 dfn 수이다.
-
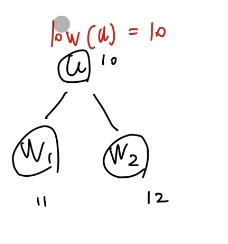
$min{low(w) w is a child of u}$ - $u$의 child vertex인 $w$들의 $low$ 값 중 가장 작은 값이다.
-
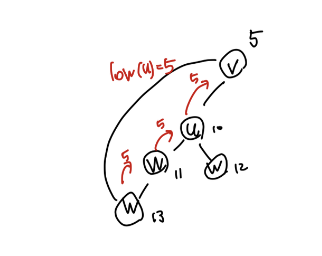
$min{dfn(v) (u,v) is a bach edge}$ - $u$의 ancestor인 $v$로 이어지는 back edge 중 가장 작은 값이다.
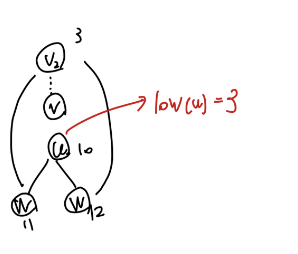
-
-
$dfn$과 $low$를 구해보면 다음과 같다.
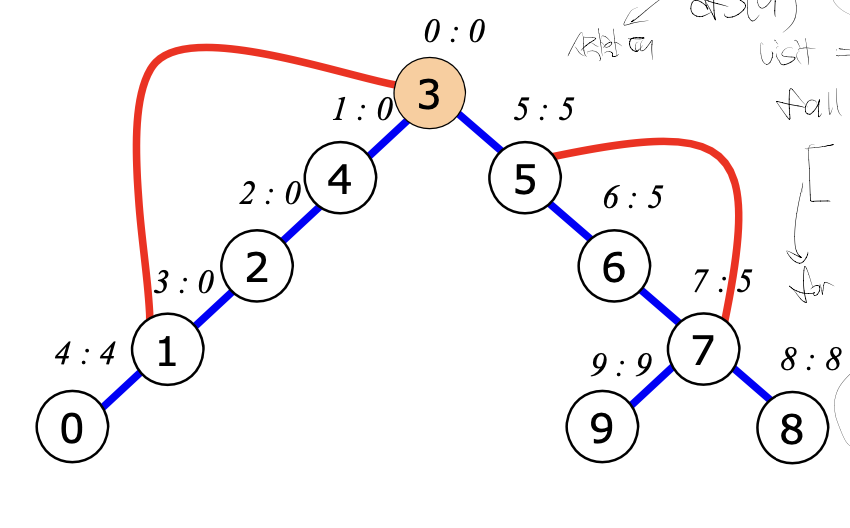
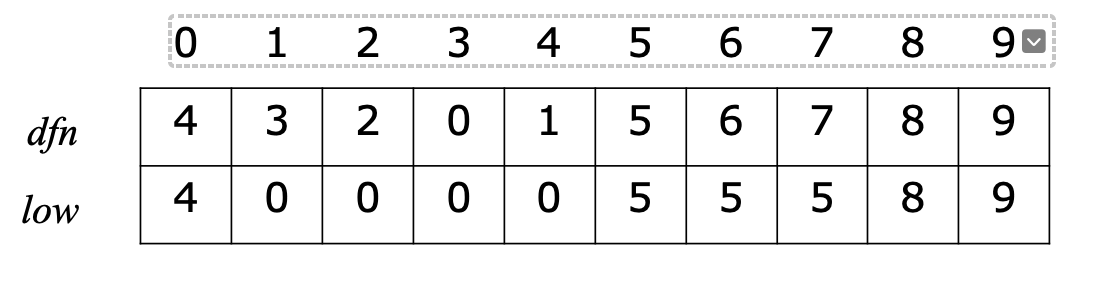
이제 두가지 규칙을 통해 분절점을 구할 수 있다.
- Tree에서 두 개 이상의 자식을 가질 경우 분절점이다.
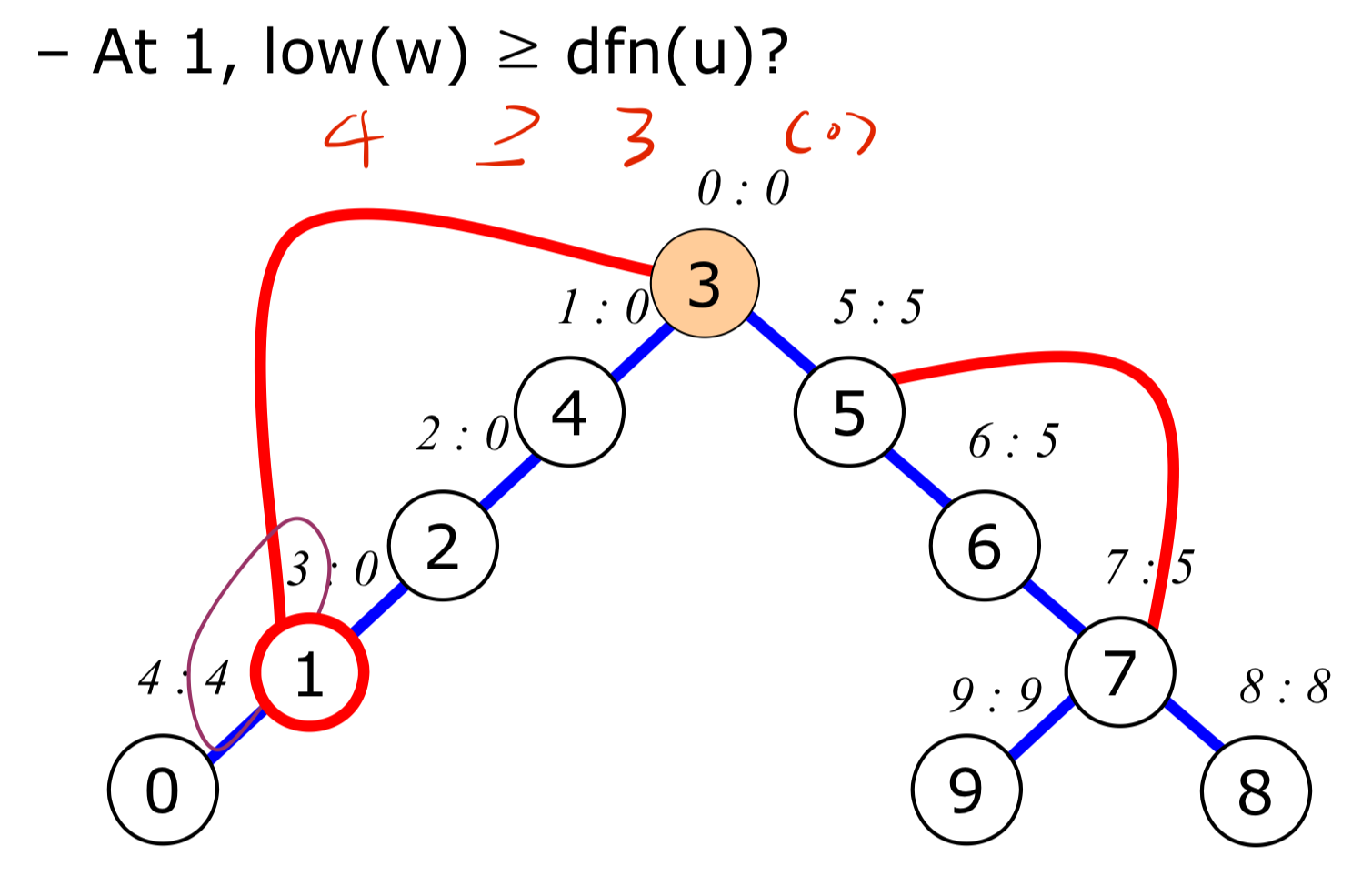
- $u$가 root가 아니고, 자식 vertex $w$의 $low(w) \geq dfn(u)$이면 분절점이다.
-
$1$ vertex는 분절점이다.
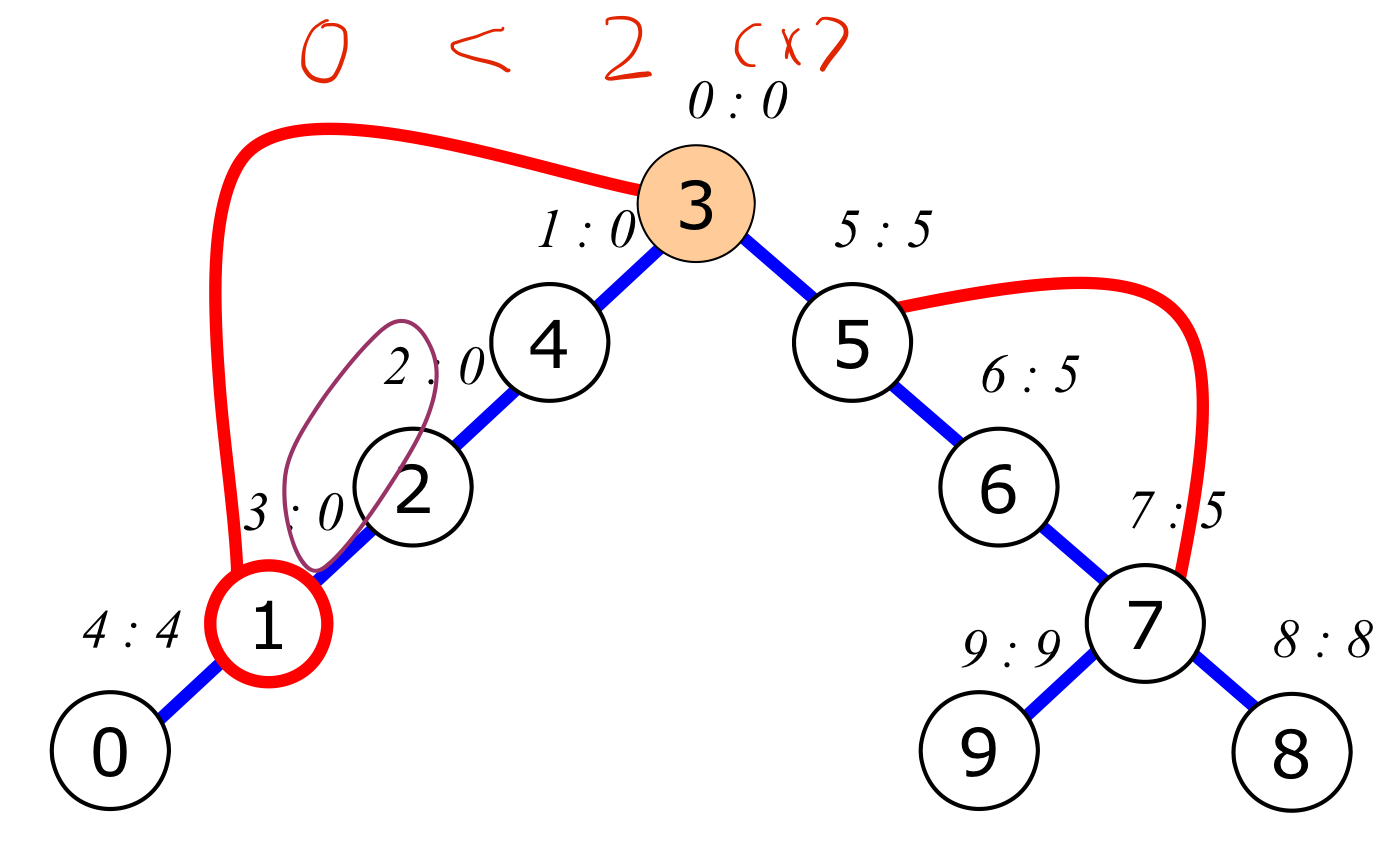
-
$2$ vertex는 분절점이 아니다.
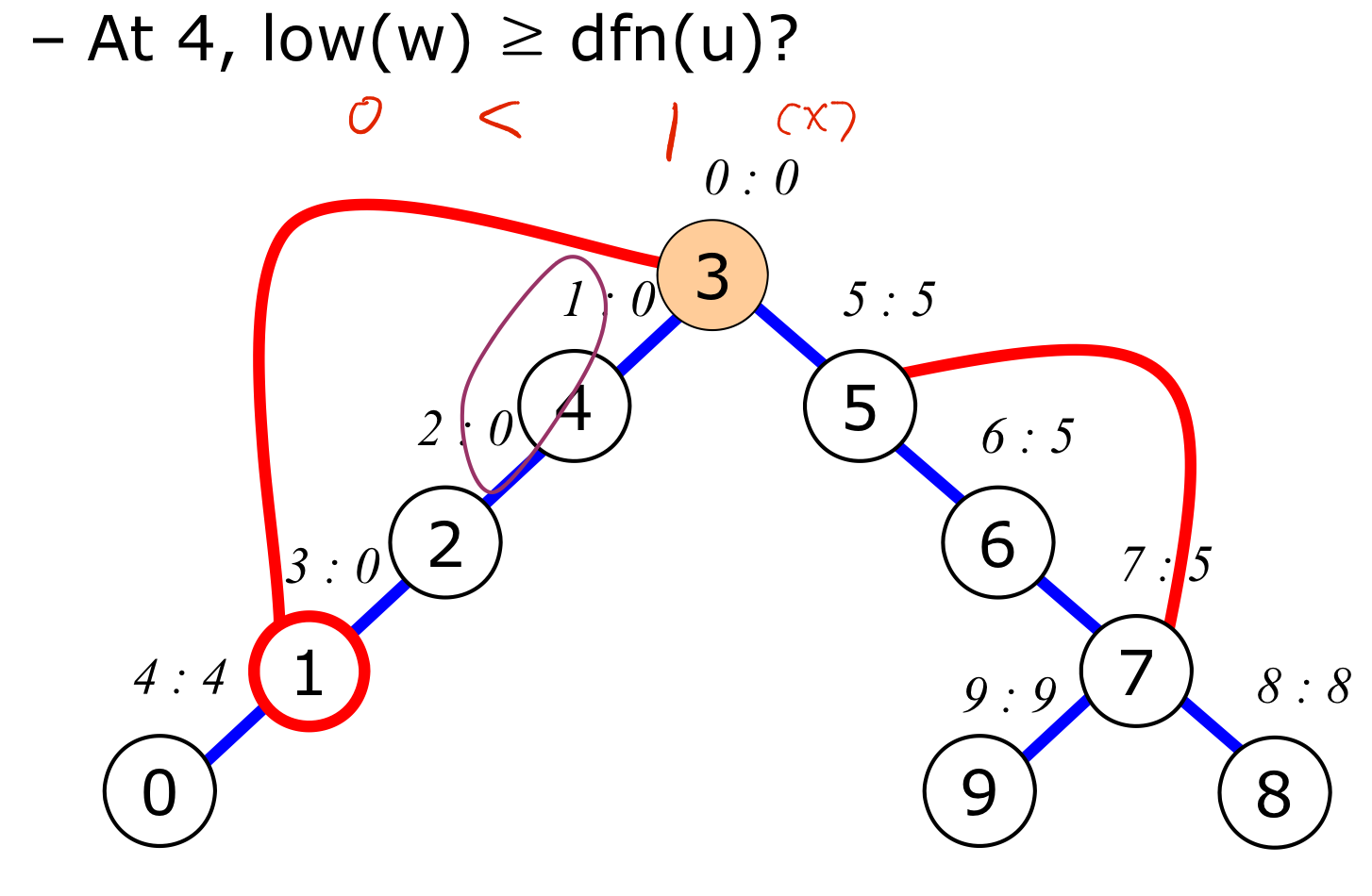
-
$4$ vertex는 분절점이 아니다.
-
$7$ vertex는 분절점이다.
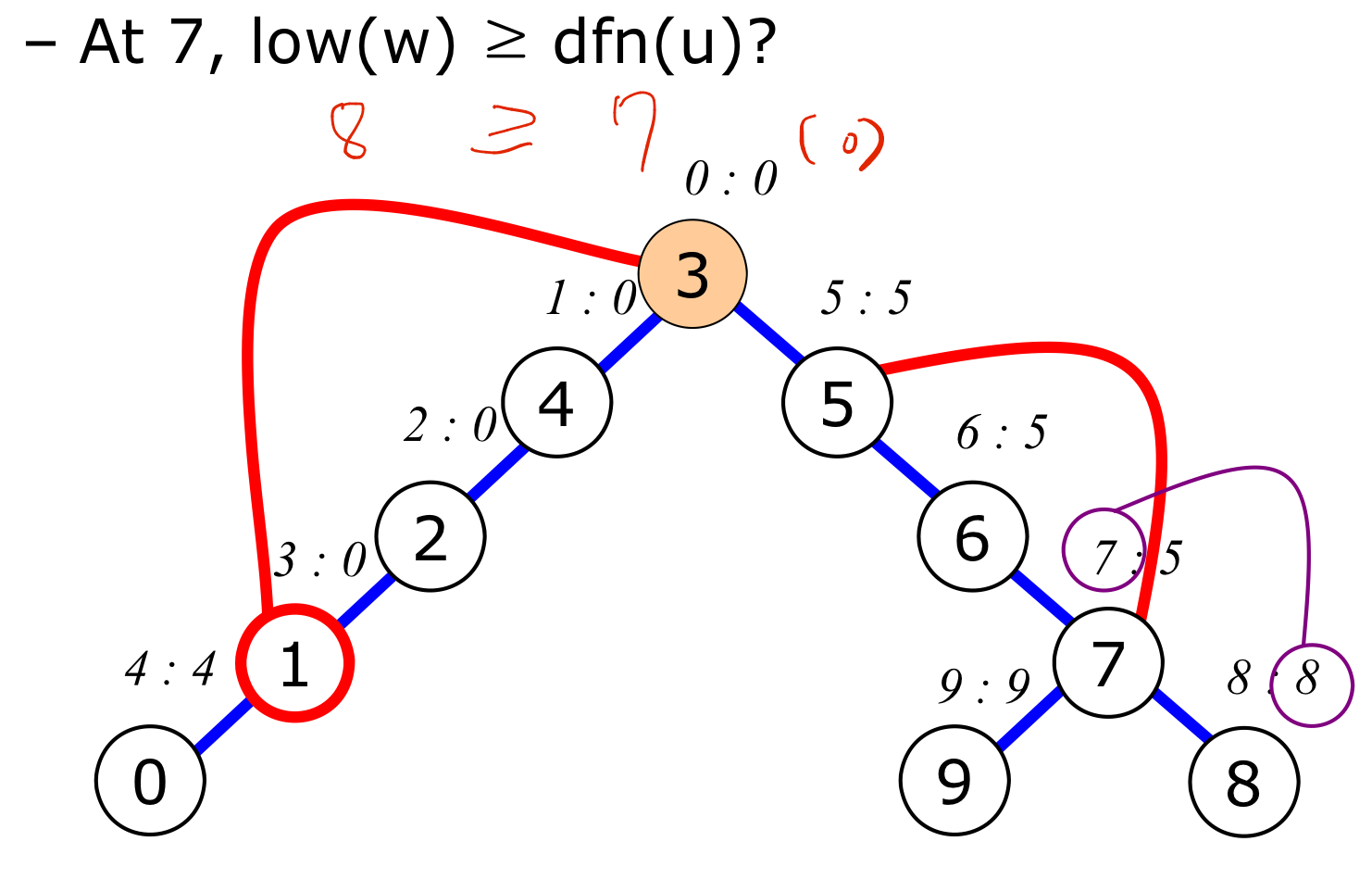
-
$6$ vertex는 분절점이 아니다.
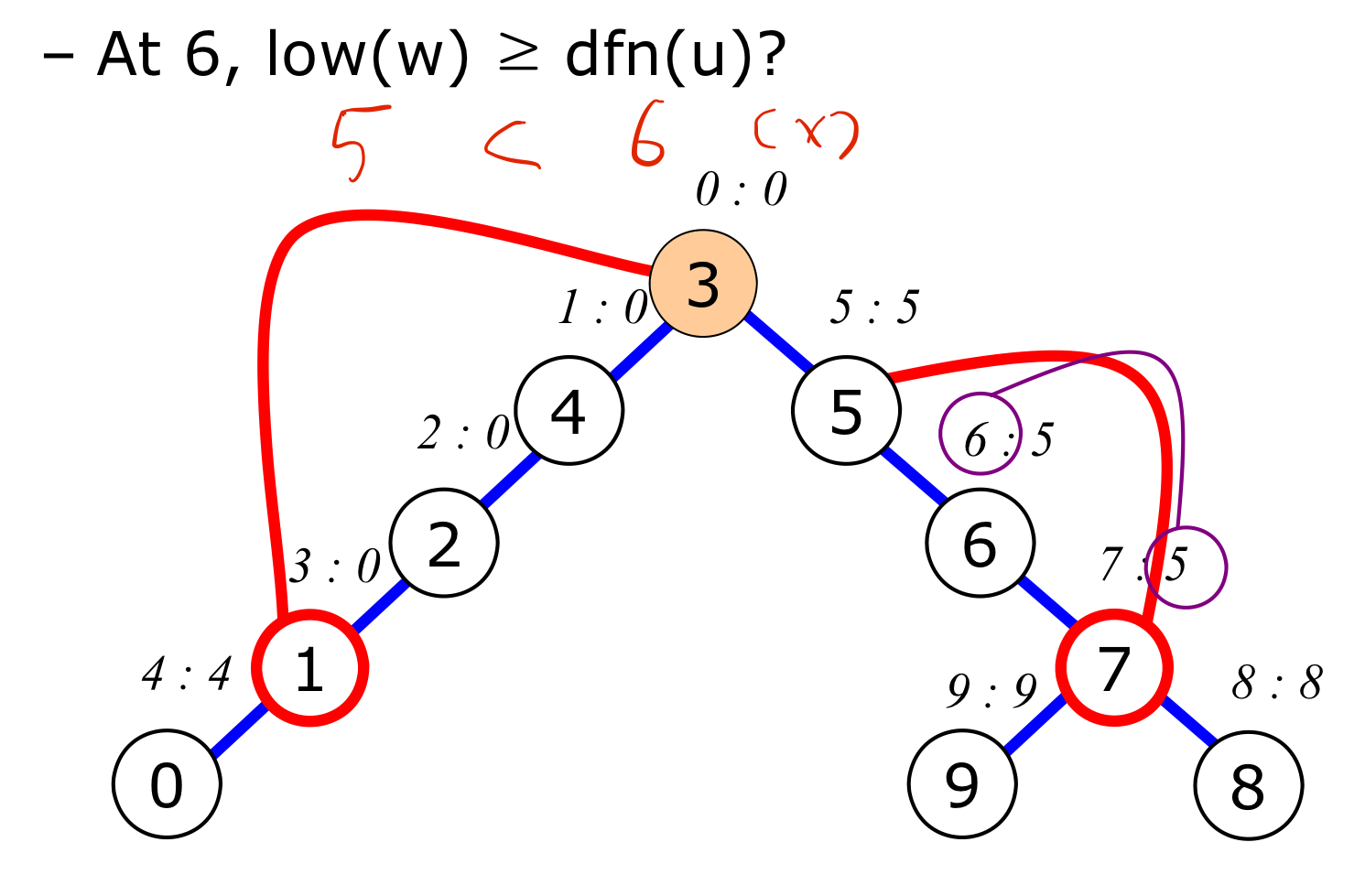
-
$5$ vertex는 분절점이다.
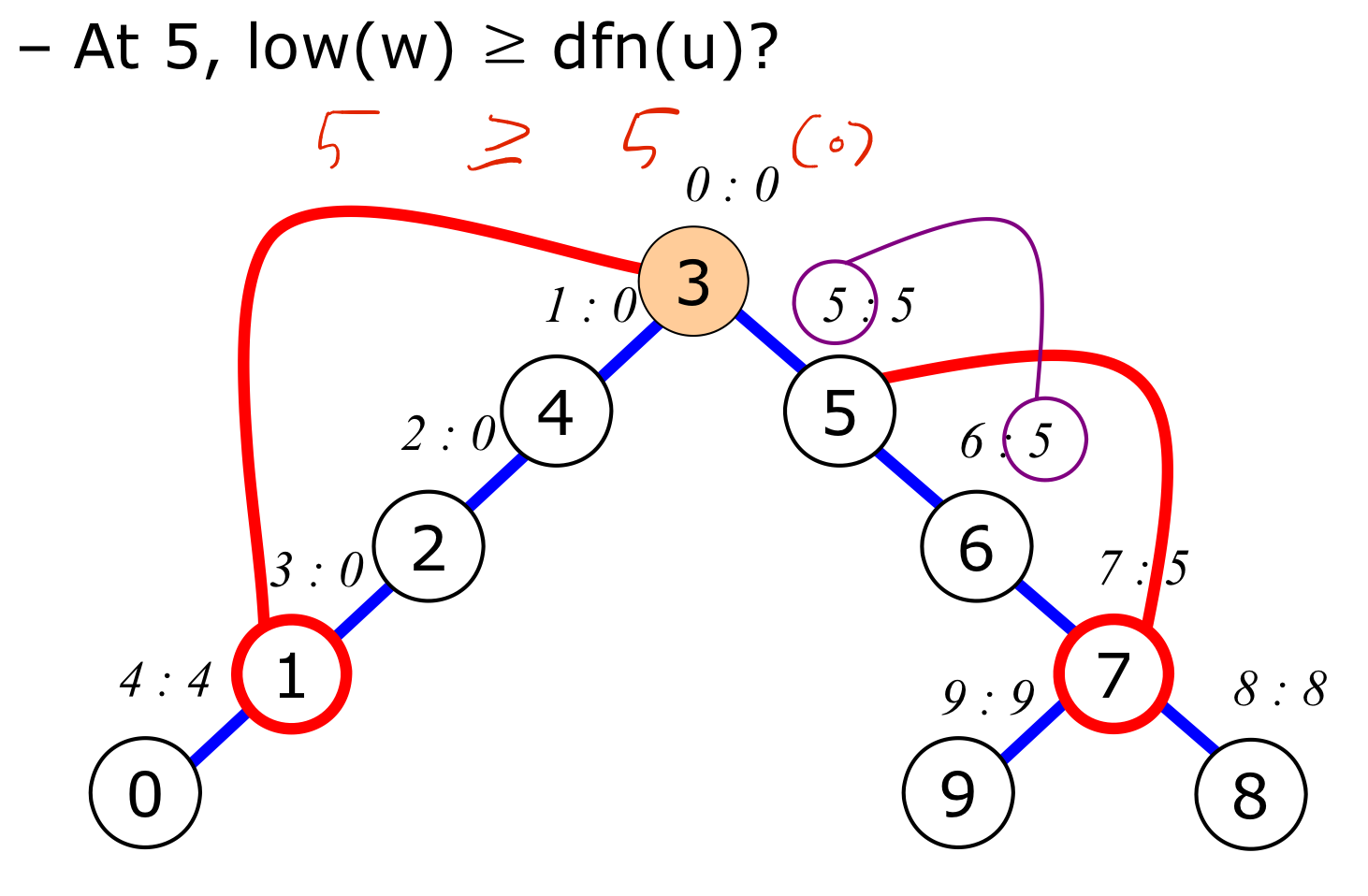
- $3$은 root이므로 분절점이다.
| 정리해보면, ${u\, | \,low(w)\geq dfn(u)} + \text{root}$ 이므로, 분절점은 다음과 같다. |
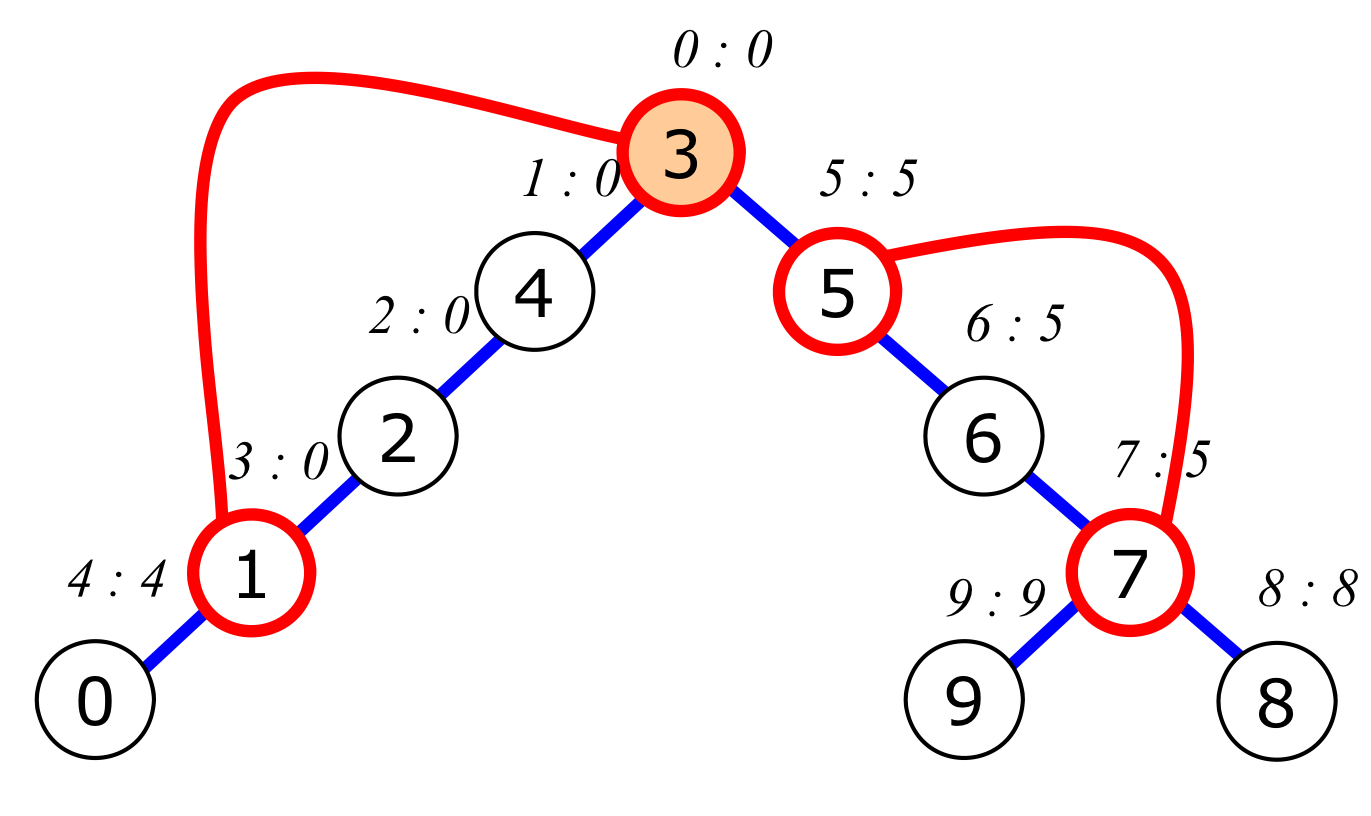
Code
BCC는 dfs를 한 번만 돌리면 dfn, low, articulation point, BCC를 전부 구할 수 있다. 즉, $O(n+m)$의 시간복잡도를 가진다.
Depth-first number 구하기
int visit[MAX_VERTEX]; // FALSE로 초기화
void dfs ( u )
{
visit[u]=TRUE;
for ( w = graph[u]; w; w = w->link )
if ( !visit[w] )
dfs ( w );
}
}
int dfn[MAX_VERTEX];// -1로 초기화
int low[MAX_VERTEX];// -1로 초기화
int num = 0;
void dfs1 (u,v) //v는 u의 부모
{
dfn[u] = num ++;
for ( w = graph[u]; w; w = w->link)
if (dfn[w] < 0 )
dfs1 (w,u);
}
}
low(u) 구하기
void dfs2 (u,v)// v는 u의 부모
{
dfn[u] = low[u] = num ++;
for( w = graph[u]; w; w = w ->link )
if (dfn[w] < 0 ) {
dfs (w, u);
low[u] = min (low[u], low[w]);
}
else if ( w != v)
low [u] = min (low[u], low[w])
}
}
Articulation Point 구하기
void dfs3(u,v)//v는 u의 부모
{
dfn[u] = low[u] = num++;
for ( w = graph[u]; w; w = w->link )
if ( dfn[w] < 0 ) {
dfs3 ( w, u );
low[u] = min (low[u], low[w]);
if ( low[w] >= dfn[u] )
print (“u: articulation point”);
}
else if ( w != v )
low[u] = min (low[u], low[w]);
}
}
Biconnected Components 구하기
void dfs4 (u, v) //v는 u의 부모
{
dfn[u] = low[u] = num++;
for(w=graph[u];w;w=w->link)
if ( dfn[w] < 0 ) {
dfs4 ( w, u );
low[u] = min (low[u], low[w]);
if ( low[w] >= dfn[u] ) {
print(“new bicon:”);
do {
pop (&x, &y);
print ( <x, y> );
} while ( x != u || y != w );
}
}
else if ( w != v )
low[u] = min (low[u], low[w]);
}
}
댓글남기기