[알고리즘으로 단단해지기] 3.그래프 (DFS, SCC)

23-12-24 6 분 소요

그래프 (Graph)

그래프는 개체들의 1:1 관계를 시각적으로 표현한 것이다. 특히 알고리즘에서 매우 중요한 개념이다.

그래프는 vertices와 edges로 구성되어 있다.
- $G=(V,E)$

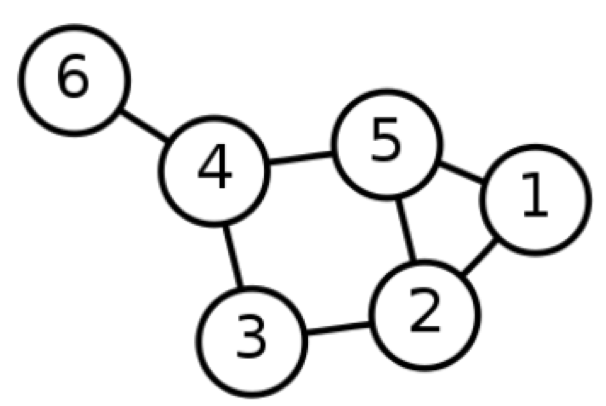
그래프는 방향성, 가중치에 따라서 4가지 종류로 나눌 수 있다.

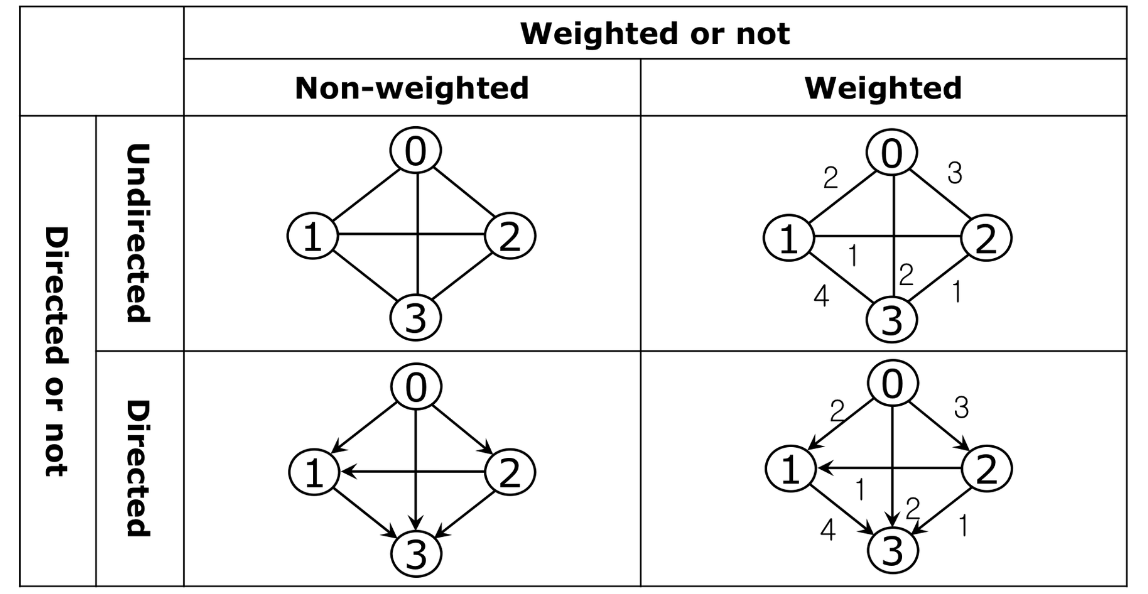
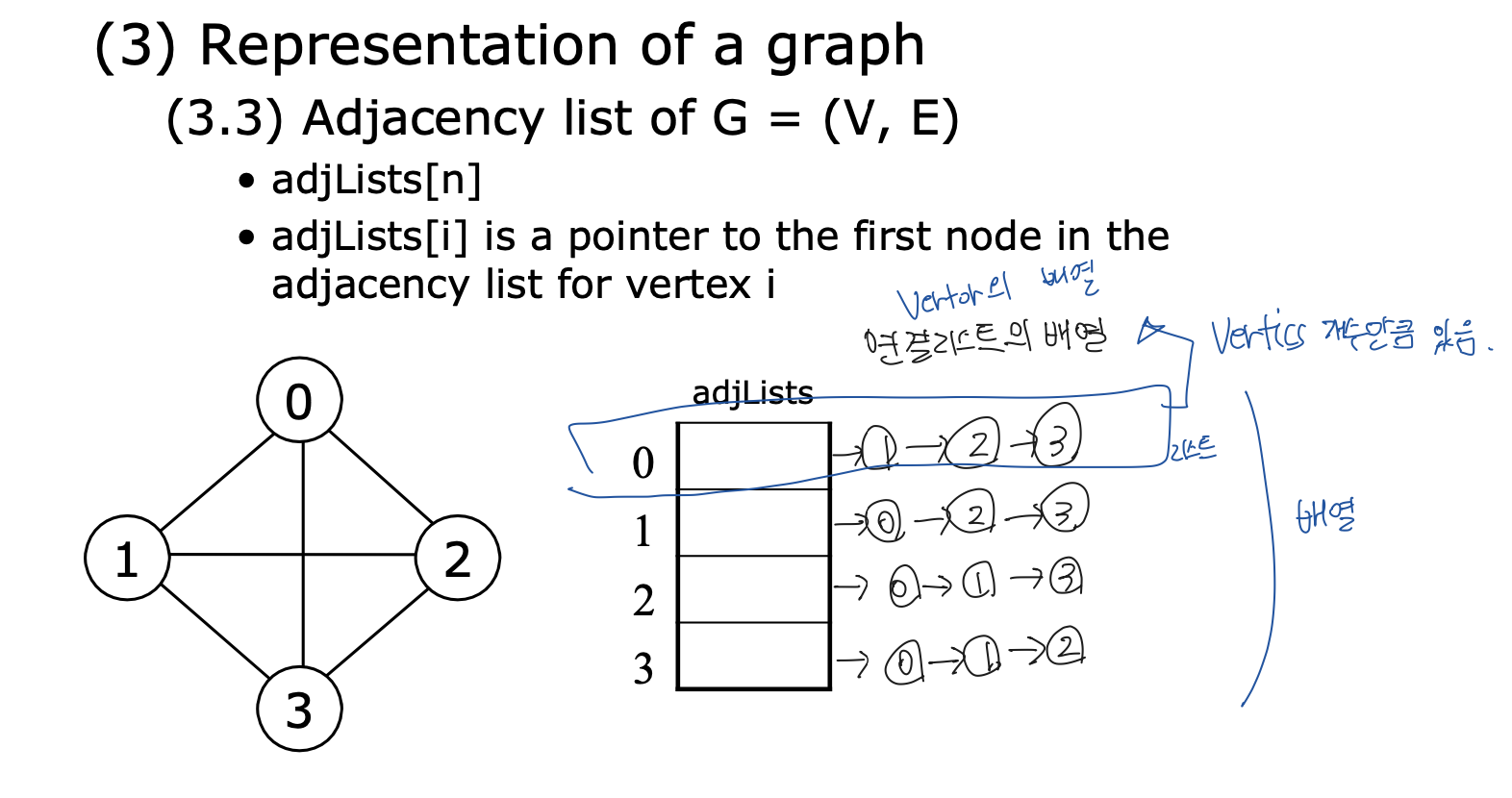
그래프의 표현

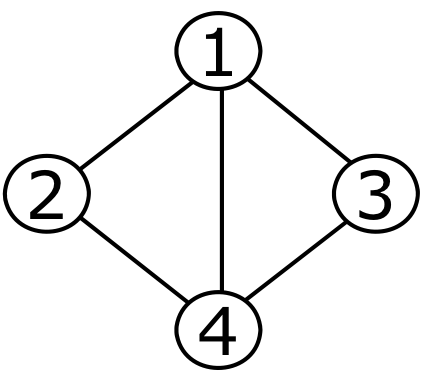
그래프의 표현법이다. 맨 위의 수는 총 vertex 수와, 총 edge 수를 의미한다.
Input:
- 4 5 // 총 vertex 수, 총 edge 수
  
  1 2 // 첫 번째 vertex, 두 번째 vertex
  
  1 3
  
  1 4
  
  2 4
  
  3 4

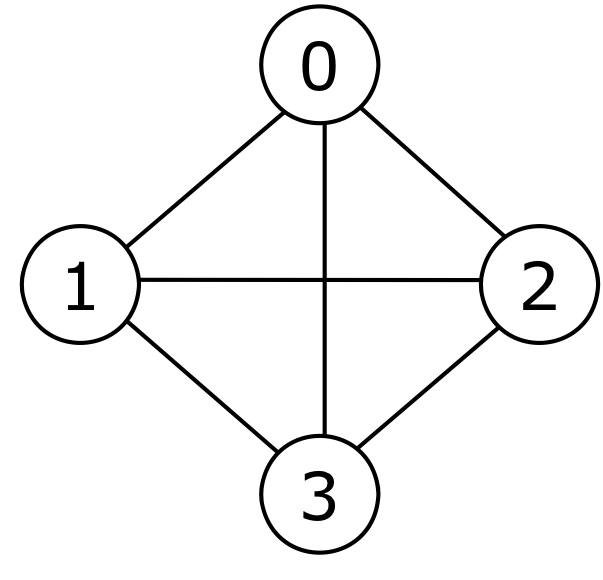
모든 vertex간 관계가 맺어져 있는 그래프를 Complete graph라 한다.

그래프의 표현 방법은 두 가지가 있다.

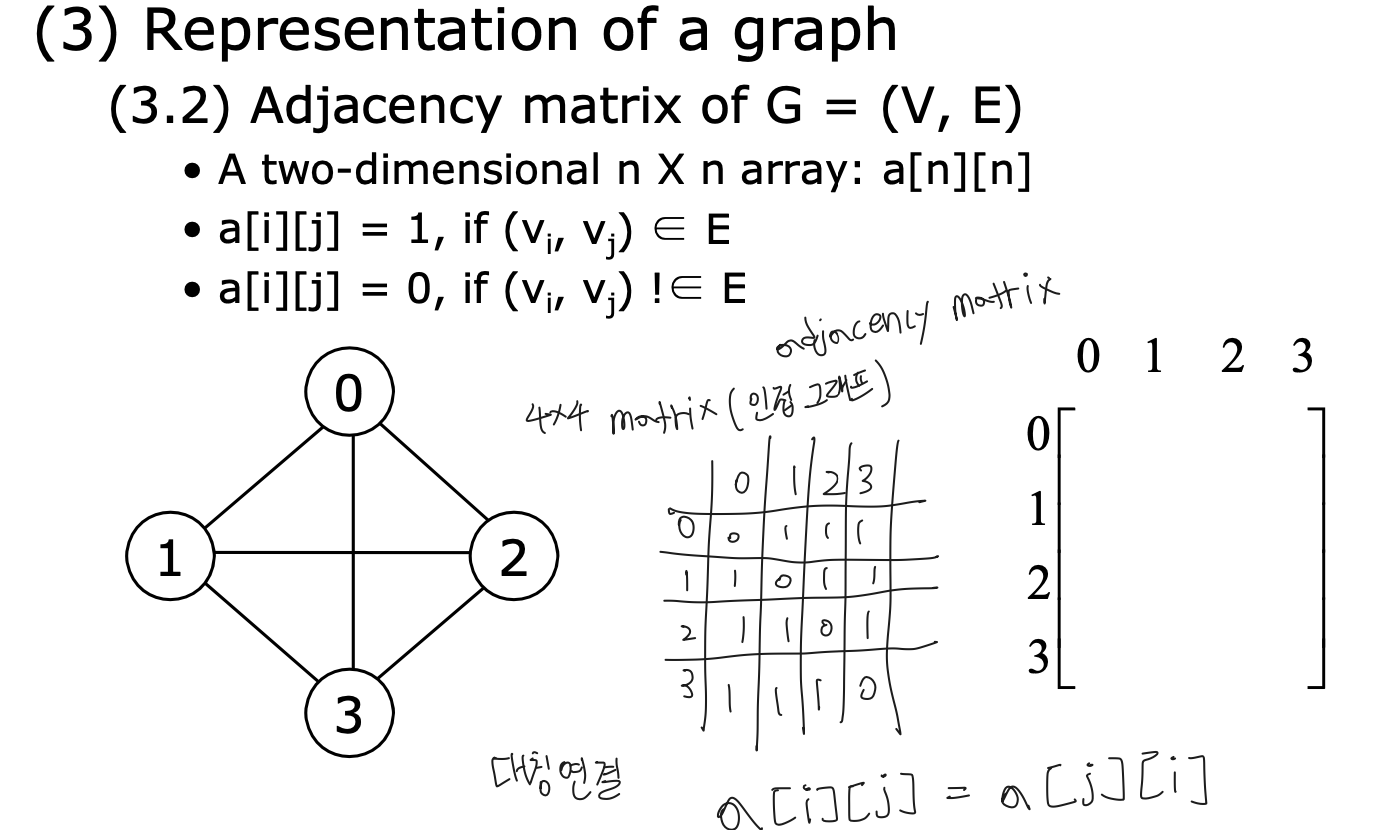
Adjacency matrix of $G=(V,E)$
- 이차원 배열로 그래프를 표현하는 방법이다.
Adjacency list of $G=(V,E)$
- Linked List(Vector)의 배열로 표현하는 방법이다.

또한, 그래프의 형태는 크게 아래와 같이 두 가지로 나뉜다.

Complete graph
- 모든 vertex끼리 관계가 맺어져 있는 그래프
- 현실에서 사실상 Complete graph를 맞이하기란 쉽지 않다.
- 또한, Complete graph의 edge는 $n^2$에 비례한다.
Sparse graph
- 일부분 vertex간 관계가 맺어져 있는 그래프
- 우리가 만나는 대부분의 그래프는 Sparse graph일 것이다.
- Sparse graph의 edge는 $n$에 비례한다.

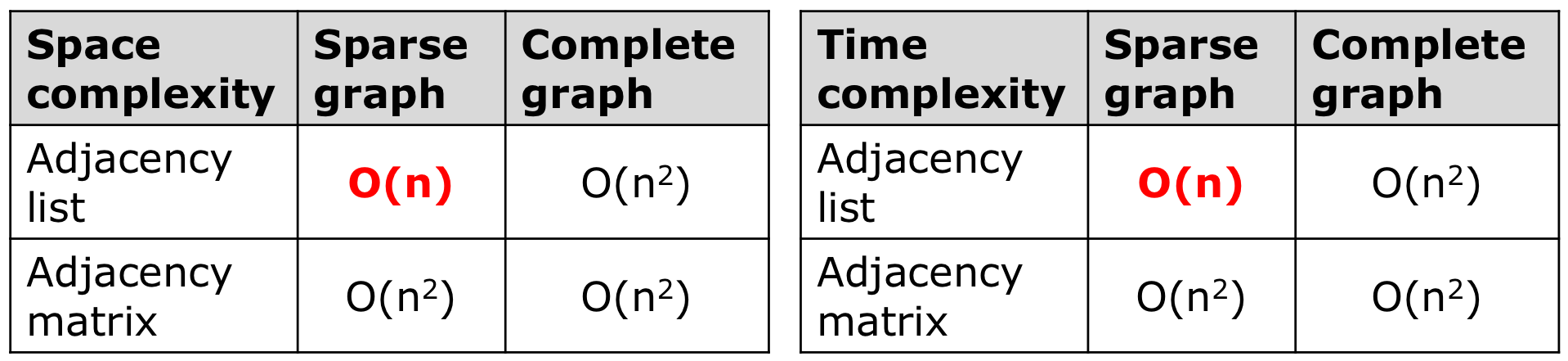
그래프의 성능

Matrix로 구현 했을 때는 Sparse, complete 의 경우 둘다 $O(n^2)$ 이다.
List로 구현 했을 때는 Sparse 의 경우 $O(n)$ 이기 떄문에 List로 구현 하는 것이 좋다.

DFS(Depth-first search)

DFS
- 깊이 우선 탐색 이다.
- 스택 기반으로 동작하며, 재귀 호출은 스택을 사용한다.
- DFS는 갈 수 있는 끝까지 간 후 pop하며 돌아오는 방식이다.

Completed graph일 경우
- $O(n+n^2) =O(n^2)$
Sparse graph일 경우
- $O(n+n)=O(n)$
따라서 edge, vertex에 따라서 바뀌기 때문에 시간복잡도는 $O(n+m)$ 이다.

Graph를 DFS Tree로 나타내기

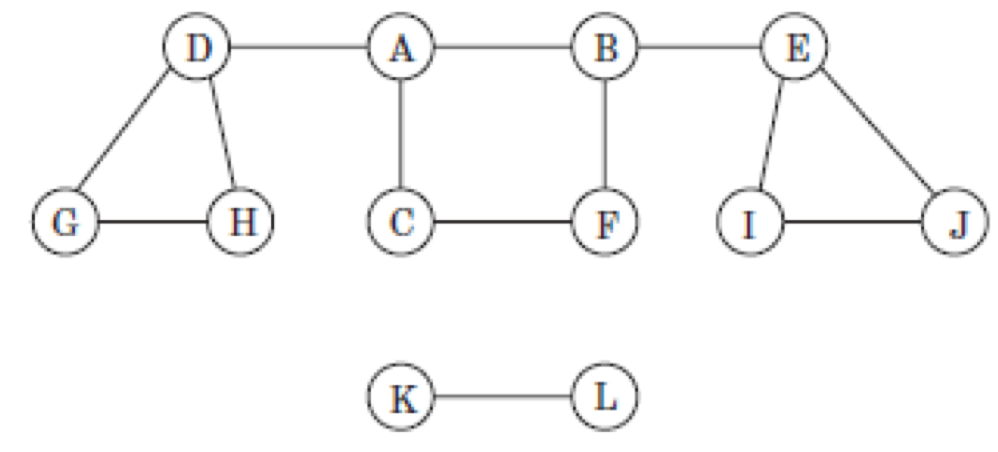
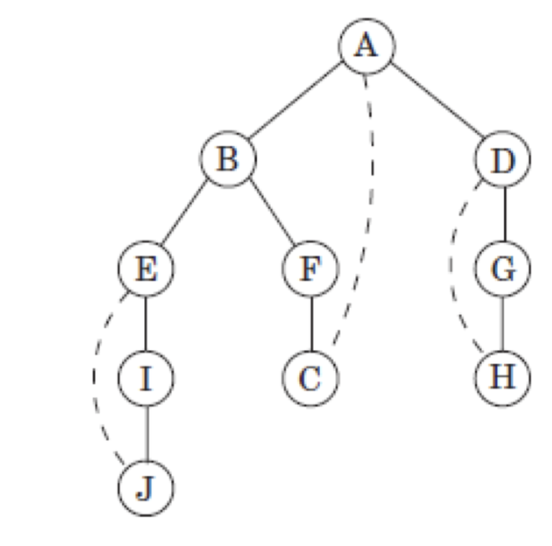
위와 같은 그래프가 있을 때, 이를 DFS로 나타내는 방법은 다음과 같다.
- 아래 예제는 순서가 명시되어 있지 않으니 알파뱃 순으로 진행한다.
  1. A와 인접한 vertex들을 가장 빠른 알파벳을 자식으로 둔다.
  2. 자식 알파뱃인 B도 가장 빠른 알파뱃을 자식으로 둔다.
  3. 더이상 자식이 없다면 pop하며 부모 vertex로 이동한다.

DFS Implementation of graph using STL

다음 문제를 코드로 표현 하면 다음과 같다.

Input:
5

2
3
4
4
4

#include <vector>
#include <algorithm>

std::vector<int> edge[10001];
bool visit[10001];

// 모든 정점에 대해 visit 배열을 false로 초기화하는 함수
void initVisit() {
    for (int i = 0; i < 10001; i++) 
        visit[i] = false;
}

// 깊이 우선 탐색 함수
void dfs(int v) {
    // 현재 정점이 이미 방문되었다면 반환
    if (visit[v] == true) {
        return;
    }

    // 현재 정점을 출력하고 방문했음을 표시
    printf("%d ", v);
    visit[v] = true;

    // 모든 인접 정점에 대해 재귀적으로 DFS 호출
    for (int i = 0; i < edge[v].size(); i++) {
        dfs(edge[v][i]);
    }
}

int main() {
    int n = 0, m = 0, u = 0, v = 0;

    // 정점 수 (n)와 간선 수 (m)를 입력
    scanf("%d %d", &n, &m);

    // 간선을 입력하고 인접 리스트를 구성
    for (int i = 0; i < m; i++) {
        scanf("%d %d", &u, &v);
        edge[u].push_back(v);
        edge[v].push_back(u);
    }

    // 인접 리스트를 정렬하여 출력 순서를 일관되게 유지
    for (int i = 1; i <= n; i++) {
        sort(edge[i].begin(), edge[i].end());
    }

    // visit 배열 초기화
    initVisit();

    // 방문하지 않은 각 정점에 대해 DFS 수행
    for (int i = 1; i <= n; i++) {
        if (visit[i] == false)
            dfs(i);
    }

    return 0;
}

자료 구조:
- edge[10001]: 그래프의 인접 리스트를 나타내는 벡터 배열이다. 각 요소 edge[i]는 정점 i에 인접한 정점들의 벡터를 포함한다
- visit[10001]: DFS 중 방문한 정점을 추적하기 위한 배열이다.
함수:
- initVisit(): 모든 정점에 대해 visit 배열을 false로 초기화한다.
- dfs(int v): 정점 v를 시작으로 하는 연결된 구성 요소의 정점들을 출력한다.
주 함수:
- 정점 수 (n)와 간선 수 (m)를 입력한다.
- 간선을 입력하고 서로를 인접 리스트에 추가하여 그래프를 구성한다.
- 인접 리스트를 정렬하여 출력 순서를 일관되게 유지한다.
- visit 배열을 초기화한다.
- 각 방문하지 않은 정점에 대해 dfs(i)를 호출하여 그래프의 모든 연결된 구성 요소를 찾아내고 출력한다.

Previsit and Postvisit Ordering

dfs 그래프에서 Previsit과 Postvisit개념을 사용하면 그래프에서 vertex간 거리가 얼만큼 떨어져 있는지 확인할 수 있다.

Previsit : 정점에 처음 방문했을 때 기록한다.
Postvisit : 정점에서 마지막으로 떠날 때 기록한다.

하위 정점에 접근하기 전 previsit에 추가하고, 모든 자식 정점들을 순회한 후 postvisit을 진행한다.

(a)에 있는 그래프를 (b)처럼 dfs규칙에 따라 spanning tree로 만들 수 있다.
- previsit과 postvisit을 숫자로 표현하면 다음과 같다.

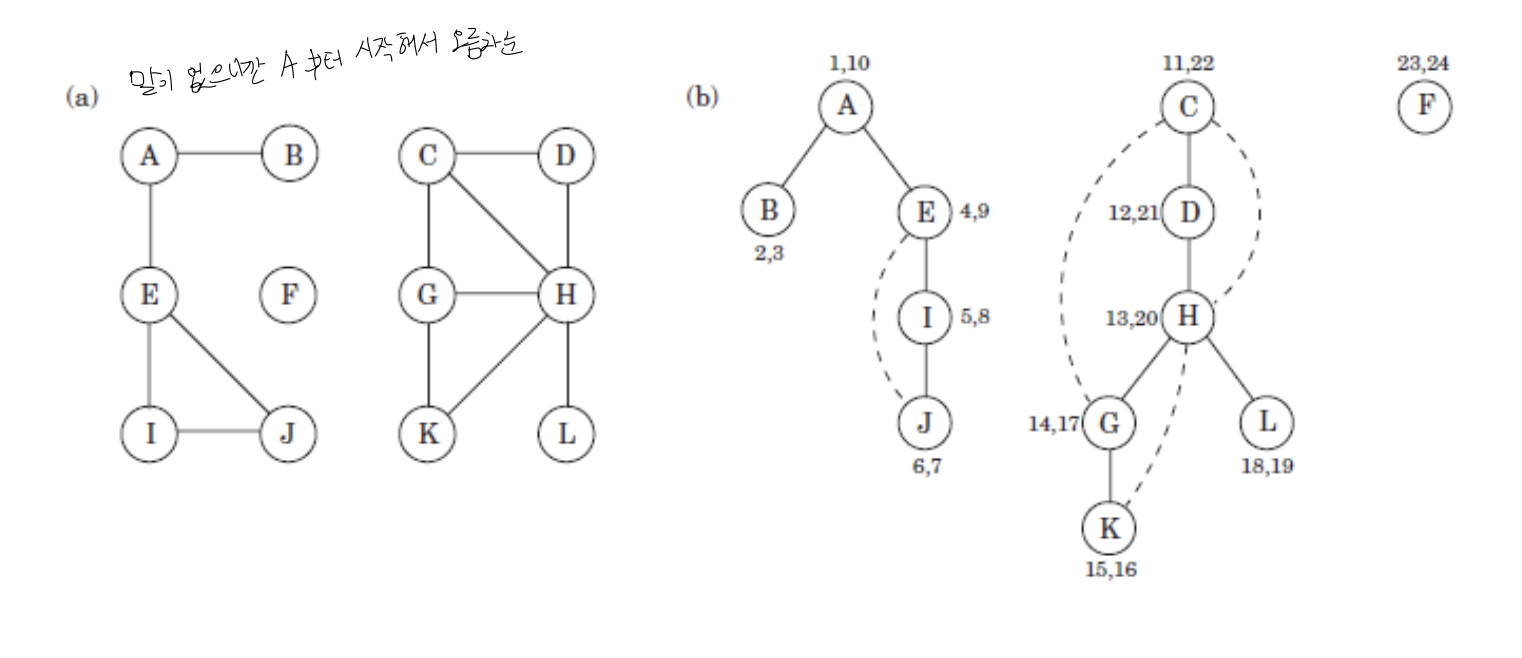
서로 겹치지 않는 번호라면 연결되어 있지 않은 정점이다.
- $G$와 $L$은 각각 (14, 17), (18, 19)로 서로 겹치지 않는다. 즉, 두 vertex는 연결되어 있지 않다.
한 정점이 다른 정점의 번호 내에 속할 경우 자식이다.
- $H$와 $K$의 경우 각각 (13, 20), (15, 16)으로 $K$가 $H$ 안에 포함된다.

Type of edges

아래와 같은 dfs 그래프가 있을 때 각 edge의 특성에 따라 4가지로 구분한다.

Tree Edge: DFS Tree안에 연결되어 있는 edge이다.
Forward Edge : 정점이 후손 정점과 연결은 되어 있으나, Tree Edge가 아닌 경우이다.
- 자식 정점은 항상 Tree Edge이므로, 자식 정점은 제외한다.
Backward Edge: 정점이 조상 정점과 연결은 되어 있으나, Tree Edge가 아닌 경우이다.
- 부모 정점은 항상 Tree Edge이므로, 부모 정점은 제외한다.
Cross Edge: 각 정점이 연결은 되어 있으나, Tree Edge가 아니어서 disjoint일 때이다.

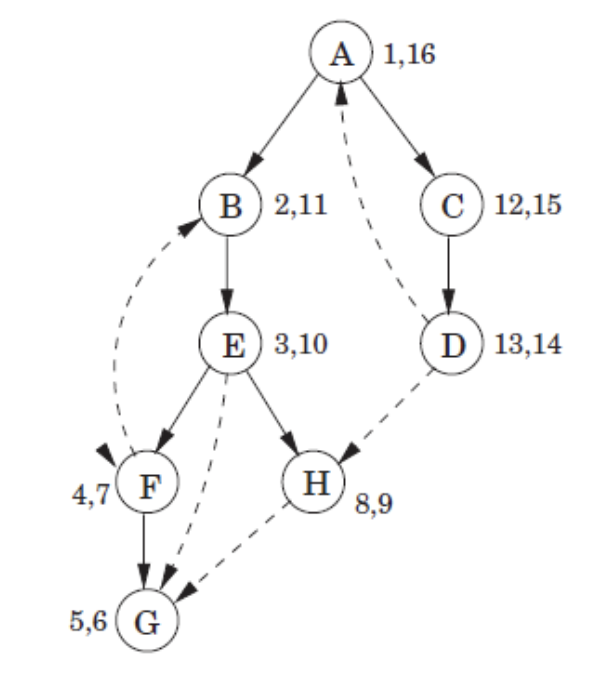
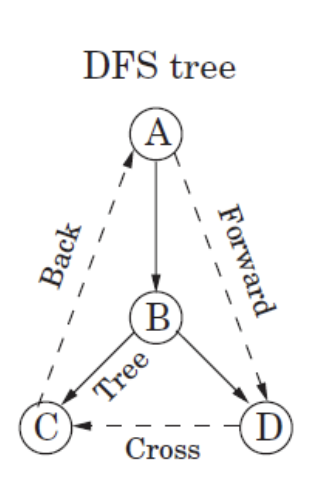
$A$와 $B,C$의 경우 Tree에 직접적으로 연결되어 있으니 Tree Edge이다.
$E$와 $G$에서 $E(3,10)$은 $G(5,6)$을 포함하고 있으므로 Forward Edge이다.
$B$와 $F$에서 $F(4,7)$이 $B(2,11)$에 포함되므로 Backward Edge이다.
$D$와 $H$에서 $D(13,14)$와 $H(8,9)$는 서로 겹치지 않으므로 Cross Edge이다.

edge <u, v>가 있다고 할 때 각 edge별 관계는 다음과 같다.

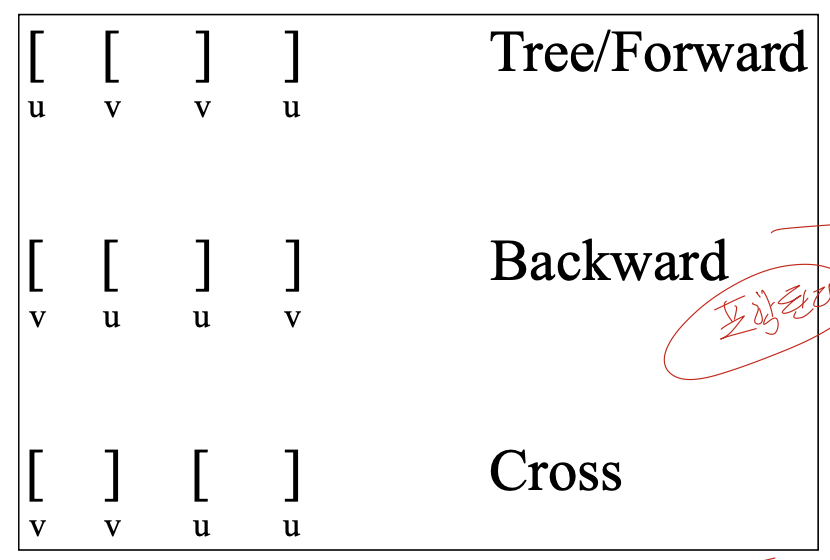
만약 $U(2, 11)$일 때 각 Edge에 따라 범위를 나타낸다면 다음과 같다.

Tree Edge : $V(3,10)$, $V(3,9)$…이다.
Forward/Bacward Edge : $V(4,9)$, $V(5,8)$ … 이다.
Cross Edge : $V(12,13)$, $V(12,14)$… 이다.

Dag (Directed Acyclic Graph)

Dag는 이름과 같이 순환(Cycle)이 없는 그래프를 칭한다.

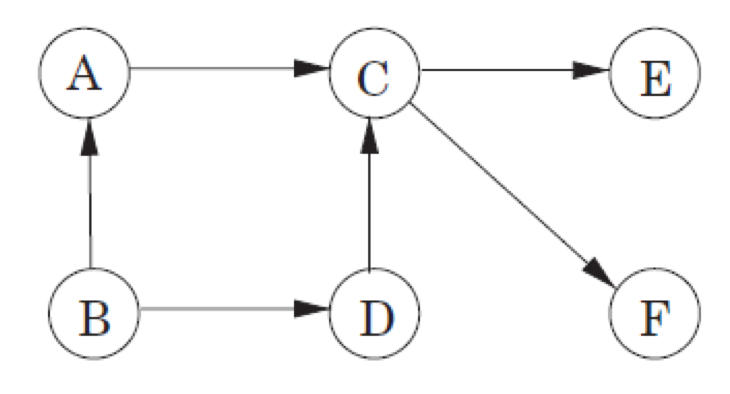
위 그래프는 어느 정점에서 출발하든 다시 자신에게로 돌아오지 않으니 Dag이다.
또한 Dag는 필수적으로 가져야 하는 두 가지 속성이 있다.
- Source(시작) : 나가는 edge만 있는 정점이다. (위 그래프에서는 $B$가 Source이다.)
- Sink(끝) : 들어오는 edge만 있는 정점이다. (위 그래프에서는 $E$와 $F$가 Sink이다.)

Source와 Sink는 둘 다 많이 있을 수는 있지만, 반드시 한 개 이상 존재해야 한다.
위 Dag에서 Source → Sink 일 때의 Topological order(한 정점에서 다른 정점까지 갈 수 있는 길을 나열한 것이다)는 다음과 같다.
- $B\rightarrow A\rightarrow C\rightarrow E$
- $B\rightarrow A\rightarrow C\rightarrow F$
- $B\rightarrow D\rightarrow C\rightarrow E$
- $B\rightarrow D\rightarrow C\rightarrow F$

Directed Graph에서 Cycle이 존재한다면 BackEdge가 존재한다.
Dag에서 부모 정점은 자식 정점보다 항상 Postvisit 이 더 크다.
- 주의할 점으로 Dag를 Tree로 나타낼 때 Previsit, Postvisit 순서를 신경써야 한다.
  - 알파벳 순으로 진행할 때 Source라고 먼저 시작하는 행동은 하면 안된다.
또한, Source가 하나일 경우 제일 높은 Postvisit은 항상 Source이다.
- Source가 두 개 이상일 경우 Source중 하나가 가장 큰 Postvisit을 가진다.
모든 Dag는 반드시 1개 이상 Source와 Sink가 존재한다.

Purpose
- Graph의 목적은 방법에 따라 항상 모든 노드를 찾아보는 것이다.
Operations
- DFS 알고리즘은 맨 마지막 정점을 우선으로 접근하며 순회한다.
- 즉, 모든 vertex들과 edge들을 방문한다.
Performance
- DFS는 보통 edge의 수($m$)에 비례해 반복하나, edge가 없는 경우 vertex의 수($n$)만큼 반복하므로 $O(n+m)$이다.

SCC (Strongly Connected Components)

그래프에서 두 vertex가 어떤 방법이든 서로 방문이 가능할 때 SCC (Strongly connected componets)라 부른다.

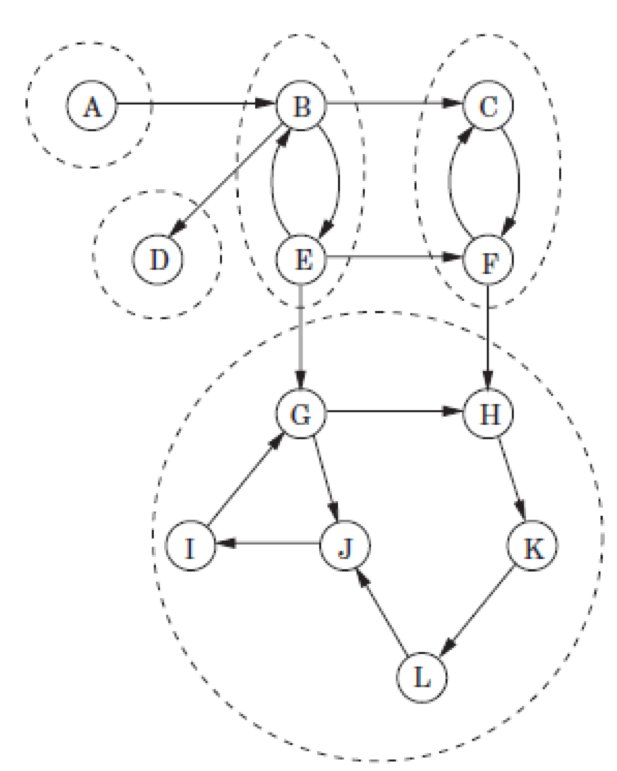
위와 같은 Directed Graph가 있을 때 SCC 그룹은 아래처럼 구분이 가능하다.
- A is SCC
- D is SCC
- B & E are SCC
- C & F are SCC
- G & H & I & J & L & K are SCC (위 그래프에서 관계가 가장 강하다.)
즉, vertex간 cycle이 존재해야 SCC가 성립할 수 있다.

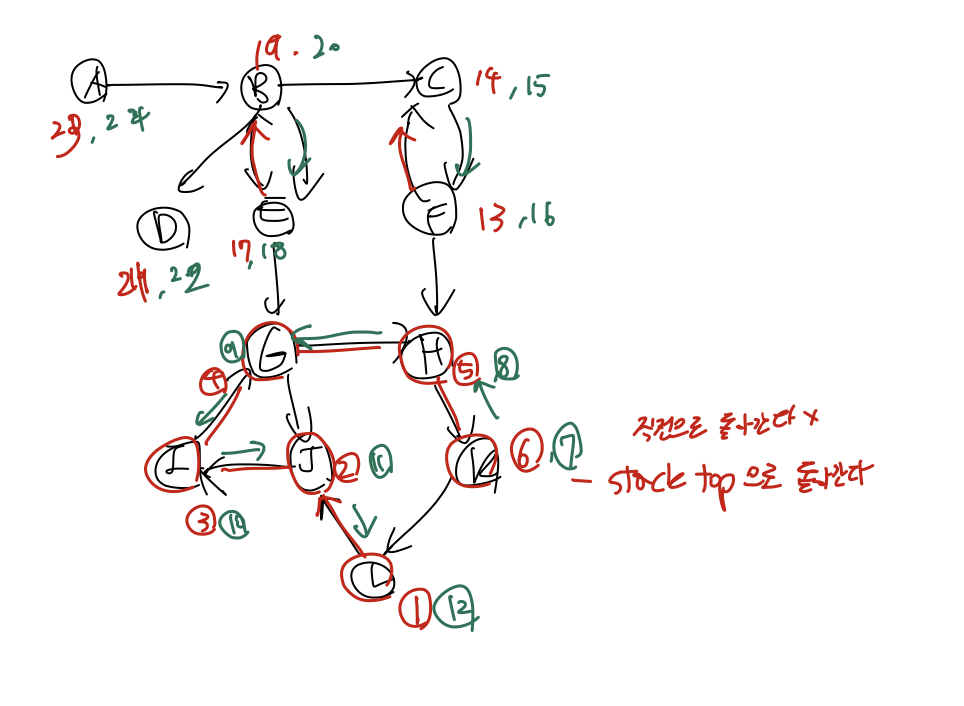
그럼 위 그래프를 previsit과 postvisit로 표현해 보자. (알파벳 역순으로 진행한다.)

그럼 SCC끼리 그룹으로 묶어 다시 그래프로 표현해보자.

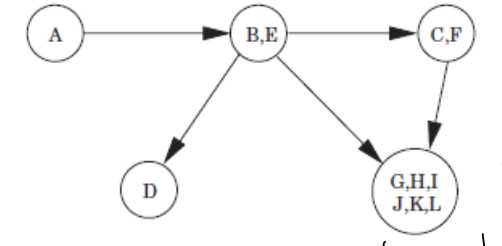
Dag의 형태이다.
- $A$가 Source이며, $D$와 $G,H,I,J,K,L$ 그룹이 Sink이다.
위 Dag에서 가장 큰 Postvisit은 Source인 $A$이다.
- $B, E$ 그룹은 $C,F$그룹, $D$ 그룹, $G,H,I,J,K,L$ 그룹보다 Postvisit이 더 크다.
- $C,F$ 그룹은 $G,H,I,J,K,L$ 그룹보다 Postvisit이 더 크다.

이에 따라 SCC (Strongly Connected Components)의 특성을 아래와 같이 정리할 수 있다.

SCC는 dfs() 를 돌리면 항상 모든 정점를 방문한다.
어느 정점에서 dfs() 를 돌려도 가장 큰 postvisit은 source이다.
1. 만약 위 그래프를 알파벳 순으로 진행해도 $A$가 (1, 24)로 가장 큰 postvisit을 가진다.
SCC를 그룹으로 나눴을 때 edge가 $C \rightarrow \bar{C}$라면 $C$의 postvisit은 항상 $\bar{C}$보다 크다.

전략 (Strategy)

dfs그래프가 주어졌을 때 SCC를 찾는 전략으로는 Sink를 찾는 것이다.

Sink를 통해 SCC를 찾고 해당 정점들을 remove한다.
1. Sink를 기준으로 dfs를 돌리면 그 정점들은 SCC이다.
1. 방법을 하나의 SCC가 남을 때까지 반복한다.

하지만, 우리는 Postvisit을 통해 Source는 구할 수 있지만, Sink를 구하는 방법을 모른다.

이에 다음과 같은 방법을 사용해 해결할 수 있다.

기존 $G=(V,E)$ 그래프를 기반으로 $G^R$ 그래프를 하나 더 만든다.
- $G^R$은 기존 그래프의 Reverse버전이다. (edge들의 방향을 바꾼다.)
- 이 때, $G$의 Sink는 $G^R$의 Source와 동일하다.

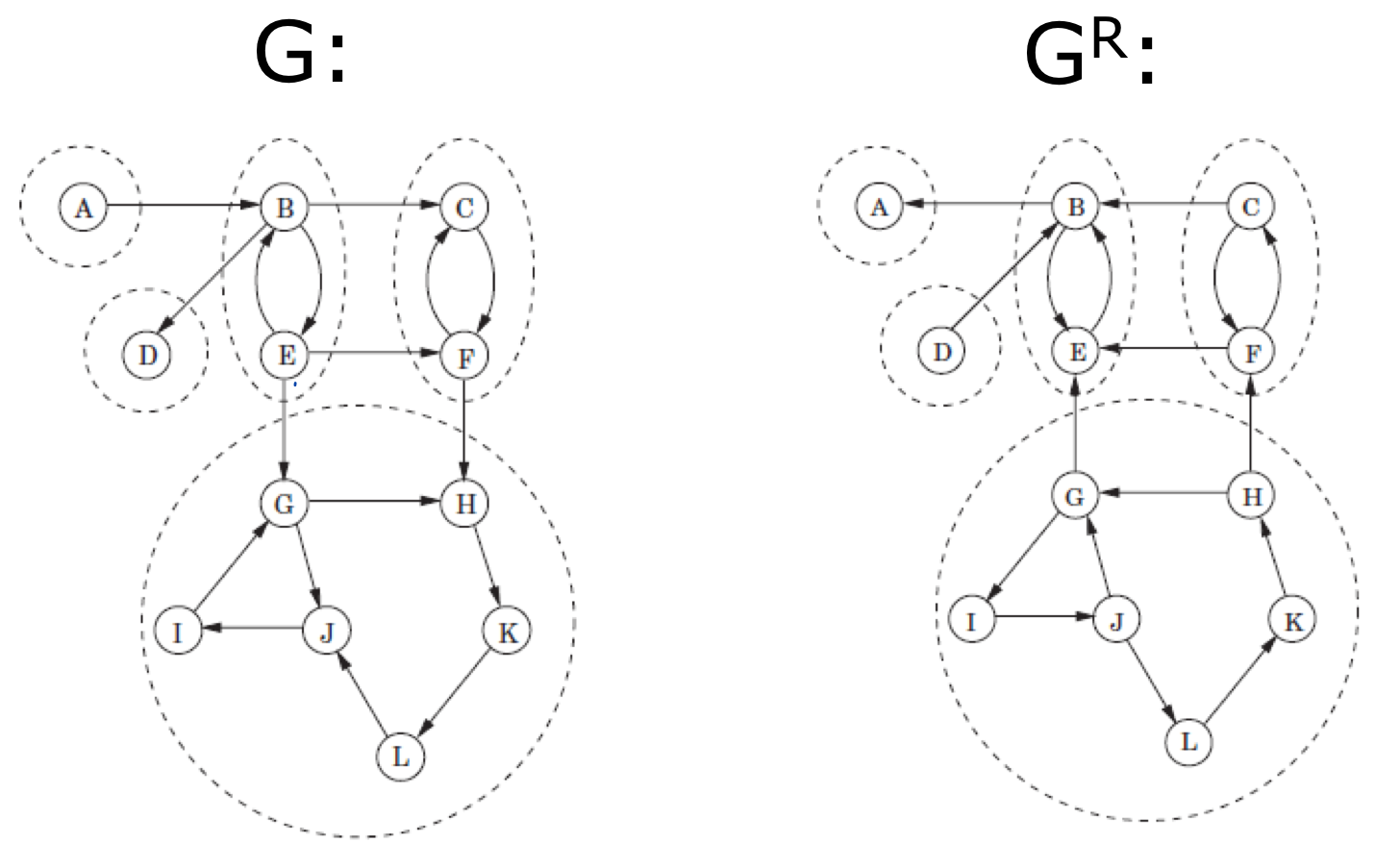
$G$와 $G^R$ 그래프를 보여준다. 두 그래프의 edge방향이 반대이다.

그럼 $G^R$에서 Source를 찾아보자. (이번엔 알파벳 순으로 진행한다.)

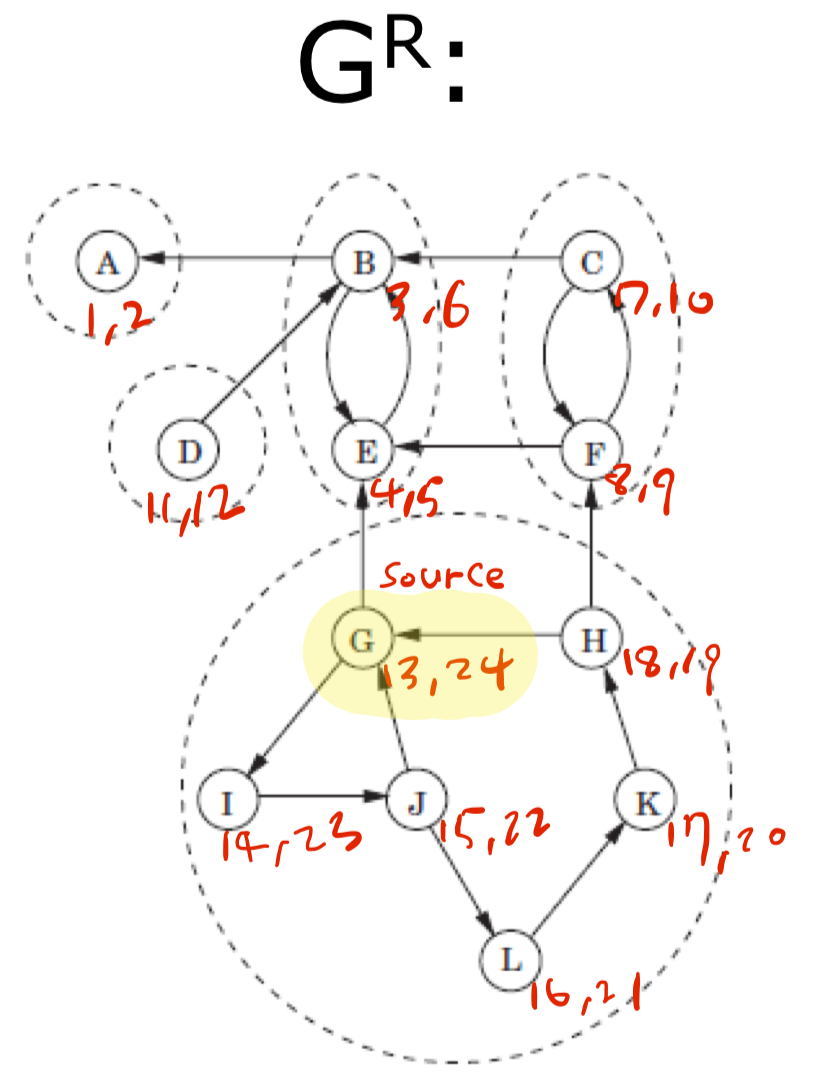
$G^R$에서 dfs()를 돌리면 정점 $G$가 Source인 것을 찾을 수 있다.
그럼 기존 $G$ 그래프에서 정점 $G$를 기준으로 dfs() 를 돌린다.
- 만약 다시 $G$를 만났다면, 그동안 거친 정점들의 부모는 $G$인 것이다. 즉, 하나의 SCC를 찾아냈다.
이후 $G^R$에서는 이전에 찾아낸 SCC를 지우고 다시 Source부터 dfs()를 돌린다.
1. 다음 Source는 $D$일 것이다. $D$는 바로 자신을 만나므로, $D$ 자체가 하나의 SCC이다.
1. 2. 방법을 반복하면 모든 SCC를 찾아낼 수 있다.

Twitter Facebook LinkedIn

[알고리즘으로 단단해지기] 3.그래프 (DFS, SCC)

그래프 (Graph)

그래프의 표현

그래프의 성능

DFS(Depth-first search)

Graph를 DFS Tree로 나타내기

DFS Implementation of graph using STL

Previsit and Postvisit Ordering

Type of edges

Dag (Directed Acyclic Graph)

SCC (Strongly Connected Components)

전략 (Strategy)

공유하기

댓글남기기

참고

[Linux] CentOS 커널 변경하기

[Linux] Shell Script

[컴퓨터네트워크] Chapter 6. Transport-Layer

[컴퓨터네트워크] Chapter 5. Network Layer