[LG Aimers] 2. Mathematics for ML

[공지사항] [해당 내용은 LG에서 주관하는 LG Amiers : AI 전문가 과정 4기 교육 과정입니다.] 강의를 듣고 이해한 내용을 바탕으로 직접 필기한 내용입니다. LG AI

2. Mathematics for ML

• 교수
  • KAIST 신진우 교수
• 학습목표
  • 본 모듈은 AI기술을 이해하기 위한 바탕이 되는 수학적 지식을 학습하기 위한 과정입니다. 이에 관하여 행렬 분해, 블록 최적화, 주성분 분석 등 데이터를 다루기 위한 방법을 학습하게 됩니다.

CHAPTER 1은 Matrix Decomposition, CHAPTER 2는 Convex Optimization, CHAPTER 3은 PCA로 구성되어있다. 이 강의를 들으면서 이해한 내용을 보다 개념적인 접근에 집중하여 소개하도록 하겠습니다.

Chapter 1.Matrix Decomposition

Matrix decomposition 행렬분해

인공지능이나 Machine Learning model을 학습하다 보면 많은 Data가 Matrix 형태로 표현되어 있는 경우가 많다.

Summary

• Determinant(행렬식), Eigenvalue(고유값)
• Cholesky Decomposition (촐레스키 분해), Diagonalization (대각화), Singular Value Decomposition (특이값 분해)

Determinant (행렬식)

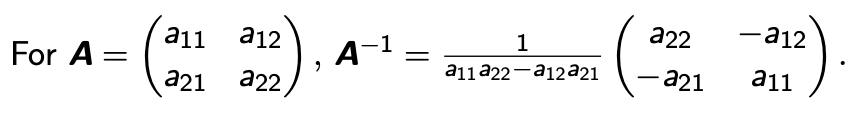
• 2 * 2 matrix와 역행렬에서 Determinant 를 알 수 있다. 이 공식에 따라 0이나 0이 아니냐에 따라서 Determinant의 존재 유무가 정해지기 때문이다.

$\alpha_{11} \alpha_{22}- \alpha_{12} \alpha_{21} \neq 0$

• 따라서 Determinant(A)는 이러한 식이 성립한다.

$det(A) = \alpha_{11} \alpha_{22}- \alpha_{12} \alpha_{21}$

---

• Lapace expansion(라플라스 전개)

  • 3 * 3 패턴의 matrix는 이 처럼 2 * 2 패턴의 Recursive formular 로 정의가 된다는 사실을 발견하였다.

    

  ---

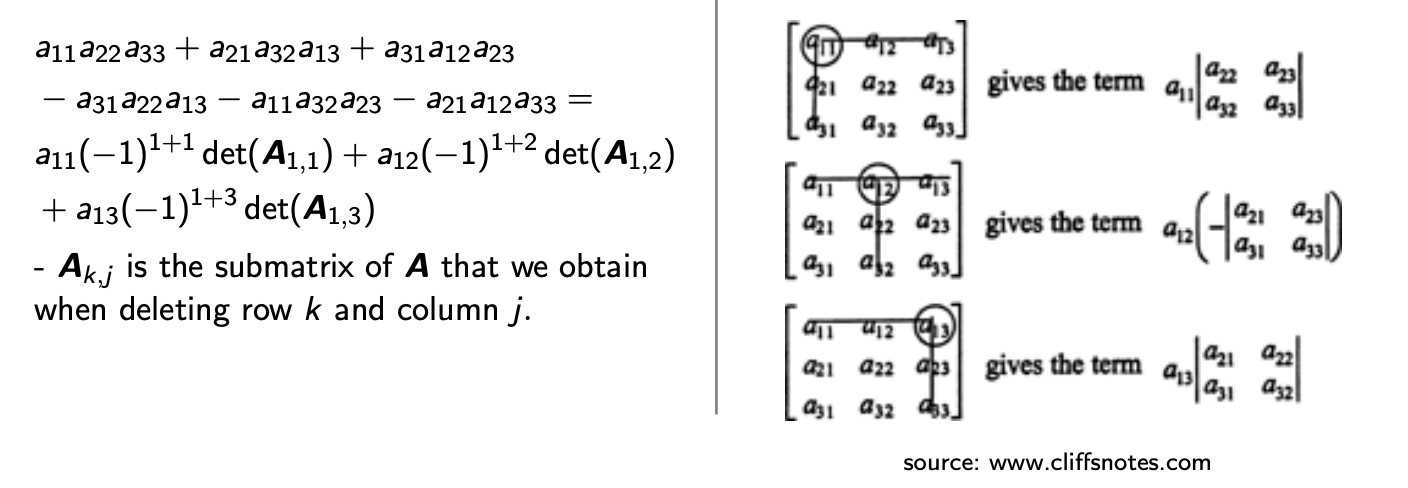
• 특징
  • 여기서 주요 특징으로는 Determinant(AB)는 곱셈에 의해서 분해 된다.
    • $det(AB)= det(A)det(B)$
    • $det(A) = det(A^T)$
    • $det(A^{-1}) = 1/det(A)$
    • $det(T) = \prod_{i = 1}^{n} T_{ii}$

Trace (행렬의 대각합)

• 정의
  • Trace는 Determinant보다 훨씬 더 정의하기 쉽다.
  • 어떤 Matrix가 있으면 Matrix의 어떤 Diagonal Entry(대각성분)를 다 더한 형태를 Trace라고 한다.
• 특징
  • 다음과 같은 성질들을 가지고 있다. Determinant는 곱셈의 성질을 가지고 있는 반면에 Trace는 덧셈의 성질을 가지고 있는 것을 알 수 있다.

• $tr(A+B)=tr(A)+tr(B)$
• $tr(\alpha A) = \alpha tr(A)$
• $tr(I_n)=n$

Eigenvalue(고유값) and Eigenvector(고유벡터)

• Determinant, Trace와 밀접한 관련이 있다.

• 정의

  • $A{x} = \lambda {x}$

  • Eigenvalue (고유값)
    • 주어진 행렬 A에 대해, 어떤 스칼라 λ(람다)가 존재하여 위의 식을 만족하는 경우, 그 스칼라 λ가 행렬 A의 고유값(Eigenvalue)이 된다.
  • Eigenvector (고유벡터)
    • 행렬 A와 그에 해당하는 고유값 λ에 대해 위의 식을 만족하는 영벡터가 아닌 벡터 x를 고유벡터(Eigenvector)라고 한다.
    • λ와 x를 찾으면, λ가 A의 고유값이 되고, x가 그에 해당하는 고유벡터가 된다.

---

• 구체적인 예제를 통해 알아보자.

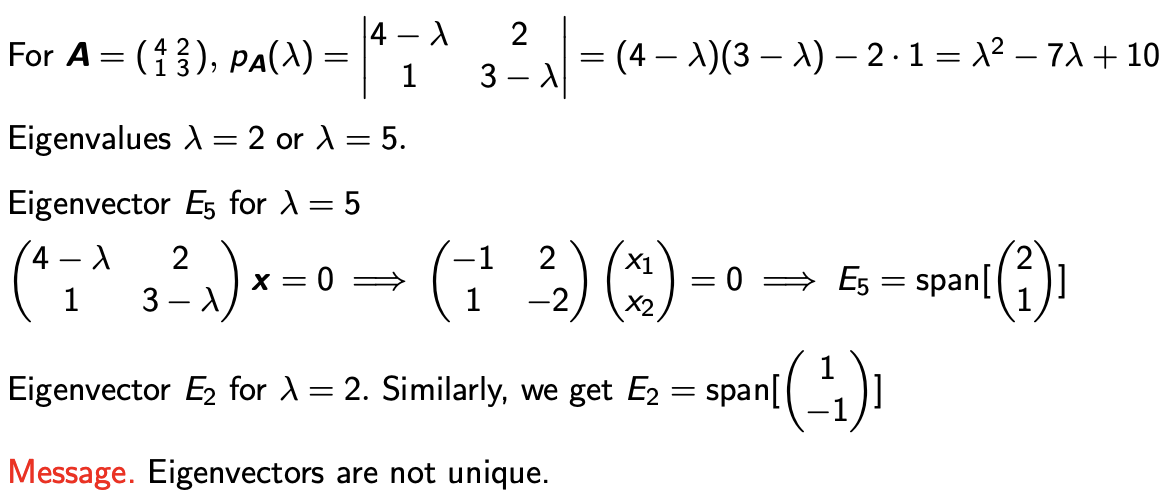
2 * 2 형태의 Matrix A에서 Diagonal Entry에 λ를 뺀후 그것에 대한 Determinant(행렬식)를 구하면 된다.

그러면 λ에 대한 2차식이 나오게 되는데 이것이 0가 되는 Solution을 구해 보면 λ=2, λ=5 를 알 수 있다. 따라서 2, 5가 Eigenvalue(고유값)이 된다.

그다음에는 2와 5에 해당하는 Eigenvector도 쉽게 구할 수 있다. Eigenvector * c 를 한 어떠한 vector도 다 Eigenvector가 된다.

이 사실을 통해 Eigenvalue는 unique하지는 않다는 사실을 알 수 있다.

결론

---

• Determinant

  • Determinant 는 이런식으로 Eigenvalue들의 곱셈으로 표현된다는 것을 알 수 있다.

  • $det(A) = \prod_{i = 1}^{n}\lambda_i$

• Trace

  • Trace는 Eigenvalue들의 덧셈으로 표현된다는 것을 알 수 있다.

  • $tr(A) = \sum_{i = 1}^{n}\lambda_i$

Choelsky Decomoposition (Choelsky 분해기법)

• Choelsky Decomoposition
  • 모든 Eigenvalue가 0보다 클때는 Matrix A가 LL^T형태로 표현된다는 것을 증명 할 수 있다.

  • 여기서 L은 lower-triangle matrix이다. 대부분의 Upper Entry 가 다 0이고 밑의 Entry만 살아 있는 것을 의미한다.

    

  • Diagonals은 positive 한 경우이다.
  • 따라서 L은 unique하고, 이런 Matrix L을 A의 Cholesky facotor 라고 한다.
• 응용
  • Decomoposition(분해 기법)을 할 수 있으면 Determinant(행렬식) 계산이 매우 쉬워 지기 때문에 사용한다.
  • Determinant 는 곱셈에 대해서 분해가 되기때문에 L곱하기 L^T 가 된다. L^T는 Determinant 성질에 의해 L로 변환되고 따라서 다음 식이 성립한다.

    • Determinant L은 lower-triangle matrix 이기 때문에 매우 구하기 쉽다.

    • $det(A) = det(L)det(L^T)=det(L)^2$

Diagonal Matrix

• Diagonal Matrix
  • 대각성분을 제외하고 0인 Matrix이다.
  • 이 Matrix의 주요 특징으로는 Diagonal Matrix의 지수승 즉, Matrix D를 k번 곱한 것들이 매우 쉽게 표현이 된다는 것이다. 대각 성분을 제외하고는 0이기 때문이다.
  • 역행렬을 구하는 것 또한 쉽다.
  • Determinant 도 Diagonal Entry에 곱셈을 하면 된다.
  • 다시 말해 Digonal Matrix는 다양한 연산들이 매우 쉽게 되는 여러가지 좋은 성질을 갖고 있다

---

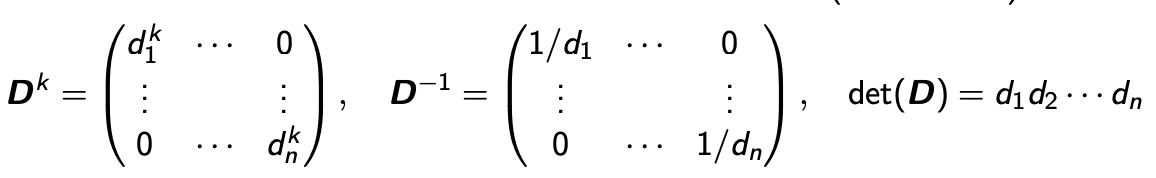
• 정의
  • 어떤 Matrix A가 있을때 D(Diagonalizable) 하게 되면 쉽게 계산할 수 있게 된다.
  • 이는 A를 대각화 행렬 D와 닮은 행렬 P를 사용하여 A = PDP^(-1) 형태로 표현할 수 있다는 것을 의미한다는 말이다.

Diagonalizable의 예를 살펴보자

• $A^k = PD^kP^{-1}$
• $det(A) = det(P)det(D)det(P^{-1}) = det(D) = \prod_i d_{ii}$

그렇다면 “어떤 Matrix가 PDP^-1로 Diagonal하게 표현 될 수 있을까?”라는 궁금증이 생긴다. 정답은.

대칭행렬(symmetric matrix)은 항상 직교 대각화 가능(orthogonally diagonalizable)하다.

결론적으로 Eigenvalue Decomposition (고유벡터 분해 기법)은 Symmetric Matrix에서만 사용할 수 있는 개념이고.

Singular Value Decomposition은 일반적인 Matrix에 적용할 수 있는 개념이다.

Singular Value Decomposition(특이 값 분해)

• 어떤 Matrix A가 주어졌을 때 임의의 행렬을 세 개의 특별한 형태의 행렬의 곱으로 분해하는 기법이다.

• 이때 U와 V^T는 항상 orthogonal Matrix(직교 행렬)가 된다는 것이 가장 중요한 특징이다.

• $A = UΣV^T$

CHAPTER 2. Convex Optimization

Convex Optimization(블록 최적화)

• Optimization은 기계학습을 이용하는 데에 매우 중요하다. 보통 ML모델을 학습한다고 했을 때 보통은 그게 Optimization 문제로 구성 되고 모델의 좋은 파라미터를 찾는 과정과 일치하게 된다.
• Machine Learning 을 하려다 보면 Optimization 문제들이 자주 등장하고 이걸 어떻게 잘 푸느냐가 좋은 Model을 찾는 것과 직결되는 문제이다.
• Optimization의 종류
  • Unconstrained optimization(제약이 없는 최적화)
  • Constrained optimization(제약이 있는 최적화)
  • Convex optimization(블록 최적화)
• Gradient
  • 즉 미분값이 0이 되는 포인트가 함수의 Minimum이 되는 경우가 많이 있다.
  • 즉 함수의 Gradient(미분) 정보가 최적화하는데 매우 중요한 역할을 하게 된다.

Optimization Using Gradient Descent

• 최적화의 목표는 보통 목적 함수 f(x)를 최소화 하는 것이 목표이다.

• 즉, 손실함수(=목적함수)를 최소화 하는 것이 좋은 파라미터를 찾는 것이다

• Gradient-type algorithms 는 다음과 같은 수식으로 표현된다.
  • Gamma K는 step size(= 학습률) 라고 부르는 어떤 Scaler 값이고

  • d는 방향성을 나타내는 Direction이 된다.

  • $X_{k+1} = X_K + \gamma_kd_k$
• 우리가 찾는 어떤 Direction d 가 어떤 Gradient와 내적 값이 0이 된다는 것은 두 벡터가 직교한다는 것을 의미한다.

Lemma: Orthogonality of Gradient and Direction

만약 어떤 방향 벡터 d 가 현재 위치의 기울기(Gradient)와 직교한다면, 이 방향에 대해서는 목적 함수를 줄이는 데 어떤 α를 사용하더라도 그 변화가 없다.

이 레마는 최적화 알고리즘에서 현재 기울기와 직교하는 방향으로 이동하더라도 목적 함수의 값이 α에 따라 변하지 않는다는 것을 나타낸다. 이는 최적화 과정에서 특정 방향으로 움직여도 목적 함수의 값이 변하지 않는다면 다른 방향으로 움직이는 것이 더 나은 선택일 수 있음을 시사한다.

하지만 이 Lemma를 긍정적으로 생각해본다면??

이 Gradient와 반대 방향으로 아무렇게나 잡기만 하면, 적절한 스텝 사이즈 α 를 선택한다면, 목적 함수를 최소화하는 방향으로 항상 이동할 수 있다는 것을 의미한다!!

Steepest gradient descent

• 현재 위치의 기울기(Gradient) 방향으로 이동하는 방법 중 하나이다. 이 방법은 각 단계에서 최대 기울기 방향으로 이동하여 최소값을 찾아가는 방법이다.
• 따라서 이 두 변환(전치와 -)를 함께 사용하여 현재 위치의 기울기의 반대 방향을 나타내고, 이 방향으로 이동하여 목적 함수를 줄이는 방향으로 움직이게 된다.

Stochastic Gradient Descent(SGD)

• Data point에 대한 Loss의 Summation 형태로 표현된다.
• Gradient update
  • Loss함수가 각각의 Data Point에 대한 Loss 함수의 합으로 표현되기 때문에 다음과 같이 표현 된다.

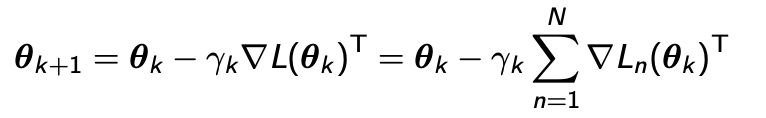
• 하지만 N, 즉 데이터가 수억개 처럼 많아진다면 이 Summation은 업데이트할때마다 매번 계산하는 것이 힘들다. 따라서 데이터 양에 따라 여러 방법으로 나눌 수 있다.

  • Batch Gradient Descent (BGD)
    • 모든 데이터를 한 번에 사용하여 그래디언트를 계산하고 파라미터를 업데이트합니다. 안정적이지만 큰 데이터셋에는 계산 비용이 높을 수 있다.
  • Mini-Batch Gradient Descent
    • 전체 데이터를 작은 미니배치로 나눠 각 미니배치에 대한 그래디언트를 계산하고 파라미터를 업데이트합니다. 계산 비용을 줄이면서도 빠른 학습이 가능하다.
  • Stochastic Gradient Descent (SGD)
    • 미니배치 크기가 1인 Mini-Batch의 특수한 경우로, 각 데이터 포인트에 대해 그래디언트를 계산하고 파라미터를 업데이트한다.

Momentum for Better Convergence in Gradient Descent

• 너무 작은 StepSize는 학습 속도를 늦추고, 너무 큰 StepSize은 발산이나 비효율적인 학습을 초래할 수 있다.
• Momentum : 해결책
  • 경사 하강법의 변형 중 하나로, 이전 업데이트의 영향을 고려하여 파라미터를 업데이트한다.
  • 현재 그래디언트와 이전 업데이트의 조합으로 새로운 업데이트 계산한다.

• $x_{k+1} = x_k - \gamma_i \cdot \nabla f(x_k)^T + \alpha \cdot \Delta x_k$

Standard Constrained Optimization Problem

• 목적함수를 최소화 하는 데에 있어서 두가지 조건이 있다고 생각해보자

  • $g_i(x) \leq 0, h_j = 0$

  • 계속 그래디언트를 업데이트를 하다보면 위 조건 0보다 작아야 하거나 0인 경우에 만족하지 않는 경우들이 나오게 된다.
  • 이러한 Constrained Optimization을 Unconstrained Optimization처럼 풀도록 한 것이 “Langrange Multipliers”이다.

Langrange Multipliers

• 라그랑주 승수를 사용하여 등식 제한 조건을 고려하는 최적화 문제를 다른 형태로 변환하는 이론이다.
• 일반적으로 최적화 문제의 목적 함수에 제약 조건을 부과하여 새로운 목적 함수를 만들고, 라그랑주 승수를 이용하여 이를 해결하는 방법을 포함한다.
• Standard Constrained Optimization Problem에서 말했던 g , h 에대한 두가지 조건을 생각해야 한다.

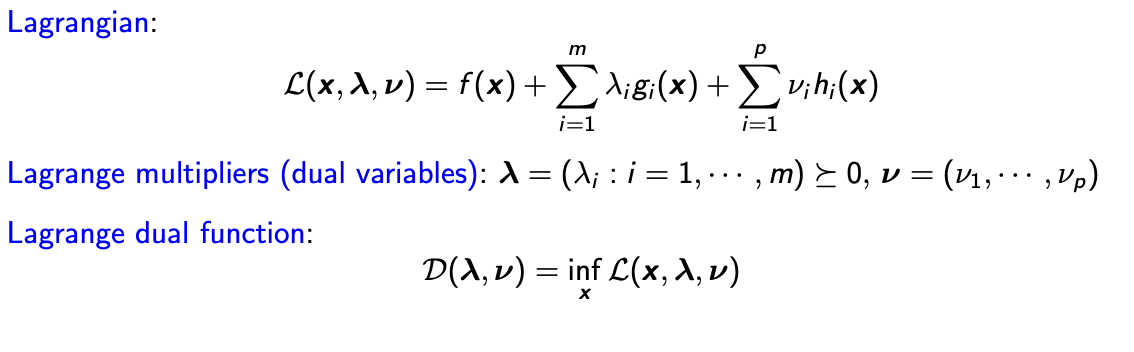
• Lagrange dual function
  • Constraint에 해당하는 조건마다 D(λ,ν)가 정의될때 이에 대한 함수이다.
  • 이런 dual function 은 항상 Convex Optimization이다.
  • 결론적으로 원래 Optimization 문제는 x에 대한 함수였는데 Lagrange dual function은 람다와 뮤에 대한 함수이다.

• 여기서 주목해야 할 사실은 dual function D 는 Optimal value인 p*의 항상 lower bound가 된다는 것이다.
  • $D(\lambda,\mu) \leq p^*$
• 그렇다면 best lower bound는 무엇일까?
  • Langrangian dual problem 문제이다. Lower bound를 Maximaization 한다고 생각해도 여전히 원래의 Optimization의 Lower bound가 되기 때문이다.
• 그렇다면 처음으로 돌아가서 Convex Optimization을 공부하는 이유는 무엇일까?
  • 모든 Optimization 문제들에 대해서 때로는 Optimization 문제가 풀릴 수 도 있고 풀리기 힘든 경우도 있지만
  • Convex Optimization문제는 항상 풀리기 때문이다!!

---

Weak Duality

• Weak Duality Theorem은 P (Primal Optimization)와 D(dual Optimization) 의 관계를 설명하는 것이다. 다음 성질을 기억 해야 한다.
  • P는 매우 풀기 힘들지만 D는 항상 풀 수 있다.
  • D는 항상 P의 Lower bound이다.

  • P와 D의 Gap 을 duality gap이라고 한다.

  • $d^* \leq p^*$

Convex Optimization

이제 이번 챕터의 주인공인 Convex Optimization에 대해서 알아보자.

• 정의
  • f(x)라는 함수를 최소화
  • f에 대한 조건을 다루는 어떤 f가 x라는 set안에 속해 있다고 가정을 한다면
  • f가 Convex function이고, x가 convex set이 될 때 Convex Optimization이라한다.
• Convex Optimization이 왜 중요할까?
  • 보통 Optimization문제가 풀린다, 안풀린다는 이 문제가 convex하냐 아니냐로 나뉜다 !

Convex Set

• 수학적으로 어떤한 Set에서 Point를 두개 잡고, 이 둘을 가르는 선분을 긋는다. 그러면 이 선분이 set안에 포함되어있을 때이다.
• 2번째 그림처럼 set안에서 나가는 경우가 생긴다면 convex set이 아니다.
• 3번째 그림또한 entry가 포함되지 않는 선분이 있기 때문에 convex set이 아니다.

Convex Functions

• 다음 식을 성립한다.
  • $f(\theta x + (1 - \theta)y) \leq\theta f(x) + (1-\theta)f(y)$

• θ를 1/2 이라고 했을 때 다음 식을 성립해야한다. 보통 볼록 함수 형태이다.

  • $f(\frac{x+y}{2})\leq\frac{1}{2}f(x)+\frac{1}{2}f(y)$

  

• Concave
  • -f 일때 convex 하다. 보통 오목 함수 형태이다.
  • 예를 들어 log 함수는 Concave이고, 음수를 취하면 Convex이다.

First -order condition

• 이것은 convex 함수를 확인 할 수 있는 한가지 방법이다.
• f가 미분 가능하다면 그래디언트를 이용하여 접선보다 함수가 항상 위에 있다면 convex하다.
• 대표적인 예로 f(y) = y^2이 있다.

Second-order condition

• Convex 함수를 확인 할 수 있는 두번째 방법이다.
• f가 두번 미분 가능하다면 두번미분한 Hassian Matrix가 Positive Semidefinite Matrix인 경우이다.
  • 쉽게 말하자면 두 번 미분 가능한 함수의 Hessian 행렬이 Positive Semidefinite(양의 준정부호) 일 때, 그 함수는 어떤 지점에서 극소값을 가질 가능성이 있다. 이는 함수가 그 근처에서 ‘아래로 볼록한(curved downward)’ 모양을 갖고 있음을 의미한다.
• First - order condition 정의와 서로 동치다.

Convex Optimization의 성질

• Convex 함수들을 선형 결합을 하게 되면 이 함수 역시 Convex하다.
• f가 Convex하다면 선형적으로 Transformation 한 다음에 f를 취해도 여전히 Convex하다.
• f1과 f2가 Convex하다면 최댓값을 취해도 Convex하다.
• 그럼 다시 되돌아가서 Lagrangian Function이 Convex 하다?
  • F(x,y)가 y가 주어져 있을 때 항상 Convex하다면 y에 대한 sup(=최소상계 = 상한값)를 취하면 이 함수도 convex하다.
    • 쉽게 말해서 어떤 함수 f(x,y)가 y에 대해서 항상 convex하다면 y값 중에 볼록한 성질중에 가장 작은 값을 선택하는 것이다.
    • Lagrangian Dual함수는 람다와 뮤에 대한 선형함수이다. 다시 말해 x를 고정할때 이 함수는 Concave 함수가 되기도 하고 Convex함수가 되기도 한다. 그래서 이것을 Infimum(= 최대상계 = 하한값)를 취해도 여전히 concave 함수라는 것이다.
      • concave함수를 최대화 하는 문제는 Convex Optimization이다. 라고 할 수 있다.

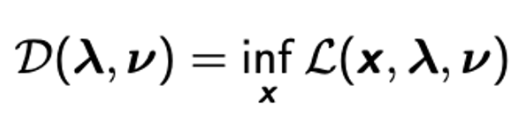
CHAPTER 3. **PCA(Principal Component Analysis)*

PCA Motivation

• 다음과 같은 2차원 데이터를 생각해본다면 x1은 매우 중요한 데이터에 대한 정보지만 x2 데이터는 거의 0에 수렴하기때문에 의미가 적은 것을 눈으로 볼 수 있다.
• 이는 ML에서 분석과 시각화를 어렵게한다. 따라서 차원 축소를 방법론을 선택하는 것이 대표적인 방법이다.

Example : Housing Data

• 집을 고를 때 다섯 가지 Feature들을 고민해야한다. 하지만 고민의 요소들이 많을 수록 어떤 요소들을 좀 더 고민 해야할 지가 복잡해 주는 경우가 있다.
• 따라서 Size, Location처럼 두가지로 줄여주는 방법론이 있다면 좀 더 수월 하게 집을 결정할 수 있다.

5 dimensions	2 dimensions
1. Size	1. Size feature
2. Number of rooms	2. Location feature
3. Number of bathrooms
4. Schools around
5. Crime rate

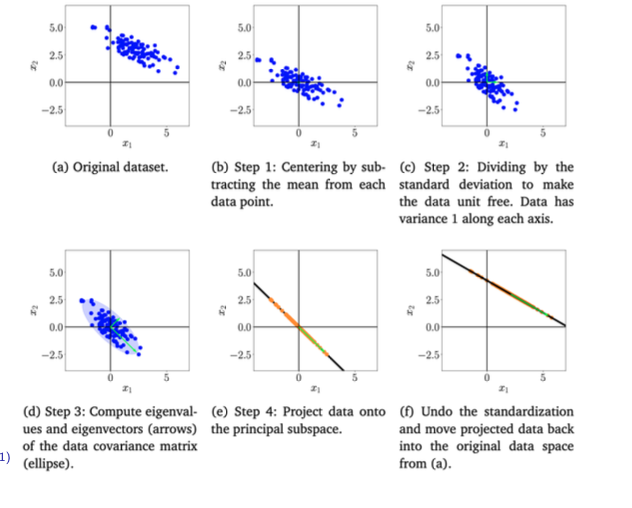
PCA Algorithm

• PCA Algorithm의 순서에 대해서 알아보자.
  1. Centerting
  1. Data의 평균을 구하고, 각 Data에 평균을 뺀다. 즉 원점을 중심으로 정렬하는 것이다.
     1. Standardization
  2. 각 차원마다 분산을 구한 다음에 그 분산으로 Data Point를 나눠주는 과정이다.
     1. Eigenvalue/vector
  3. Data Covariance Matrix에 Eigenvalue와 Eigenvector를 구하는데 그중에 M개의 제일 큰 Eigenvalue와 그것에 해당하는 Eigenvector를 구한다. 이때 M은 우리가 축소하고 싶은 차원의 개수이다. 이에 대한 개념은 뒤에서 좀 더 자세히 설명하겠다.
     1. Projection
  4. Eigenvector들이 이루는 공간을로 Data Point를 Projection(투영) 시킨다.
     1. Centering, Standardization의 역연산

Data Covariance Matrix

• N : 데이터의 개수, D : 데이터의 차원 이라고 할 때, Covariance matrix는 다음과 같은 수식이다.
• 항상 Positive Definite(양의 정부호) 된다.
  • $S = \frac{1}{N}XX^T$

• 결국 PCA 가 하는 것은 Orginal x가 있을 때 이것을 어떤 B라는 행렬을 곱해서 차원을 축소시킨다. B라는 matrix가 Orthonormal(직교) 하다고 가정했기 때문에 다시 B^T를 곱하면 원래 공간에 재구성된 데이터가 나온다.
• 결국엔 PCA는 선형적인 인코딩, 디코딩을 하는 과정이다.

PCA의 수학적 증명

• X : Original Data Point 를 의미한다
• B : 저차원 공간으로 Mapping하는 어떠한 행렬
• D : Mapping 된 Vector
• Z : 새로운 좌표
• M (축소시키기위한 차원) ≤ D(원래 차원)

• z에 대한 분산을 최대화하는 B를 골랐을 때의 Progiection Matrix를 찾는 문제에서 Data Covariance Matrix의 Eigenvalue와 밀접한 연관이 있다는 것을 수학적 귀납법을 통해 증명해 보겠다.

• 단계 1: 첫 번째 주성분 b1을 찾는다.
  • 데이터를 1차원으로 투영하여 분산을 최대화하는 벡터를 찾는다.
  • 이 벡터는 데이터 공분산 행렬의 가장 큰 고유값에 해당하는 고유벡터임을 확인한다.
• 단계 k: k번째 주성분 bk를 찾는다.
  • 이전의 주성분들과 직교하면서 k-D 평면에 데이터를 투영하여 분산을 최대화하는 고유벡터를 찾는다.

1. 고유벡터 계산 방법:
   • EVD(고윳값 분해) 또는 SVD(특이값 분해) 방법을 사용하여 계산한다.
   • 고윳값과 특이값을 활용하여 고유벡터를 찾는다.
2. 주요 고려 사항:
   • 데이터 공분산 행렬: 데이터 간의 상관 관계를 이해하고 주성분을 찾기 위해 사용된다.
   • 고유값 순서화: 고유값의 크기에 따라 해당하는 고유벡터를 순서화하여 주성분을 결정한다.
3. PCA의 활용:
   • 데이터 시각화, 차원 축소, 특징 추출 등에 활발히 활용된다.
   • 데이터의 차원을 줄이고 중요한 정보를 보존하여 더 효율적인 데이터 처리 가능하다.