[LG Aimers] 4-1. Supervised learning (classification/regression)

[공지사항] [해당 내용은 LG에서 주관하는 LG Amiers : AI 전문가 과정 4기 교육 과정입니다.] 강의를 듣고 이해한 내용을 바탕으로 직접 필기한 내용입니다. LG AI

4-1. 지도학습(분류/회귀)

• 교수 : 이화여자대학교 강제원 교수
• 학습목표
  • Machine Learning의 한 부류인 지도학습(Supervised Learning)에 대한 기본 개념과 regression/classifiation의 목적 및 차이점에 대해 이해하고, 다양한 모델 및 방법론을 통해 언제 어떤 모델을 사용해야 하는지, 왜 사용하는지, 모델 성능을 향상시키는 방법을 학습하게 됩니다.

CHAPTER 1. Linear Regression

Linear models

• Hypothesis 함수(가설함수) H가 입력 feature와 모델 파라미터의 linear conbination으로 구성된 모델이다.

• 수식을 보면 세타와 x의 내적연산으로 나타 낼 수 있다.

  

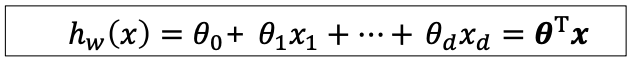
• 이 모델에서 유의점은 선형 모델이라고 해서 반드시 입력 변수의 선형일 필요는 없다.

• 모델이 단순하기 때문에 성능이 높지 않더라도 다양한 환경에서 안정적인 성능을 제공할수 있다.

  • Regression과 Classification에서 둘 다 사용 가능하다.

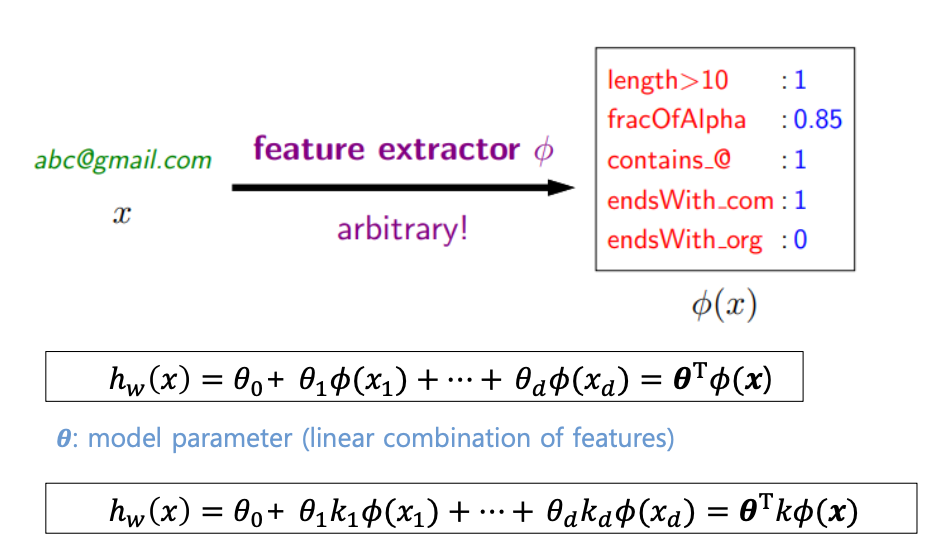
• 입력 데이터로 메일 주소 x를 받았다고 할 때 x로부터 여러 feature를 뽑는 과정
  • 입력 feature로 부터 세타와의 linear combination을 가지고 hypothesis함수를 구성할 수 있다.
  • x 는 각 feature를 의미하고 세타는 모델의 파라미터(가중치)를 의미한다.

Linear regression framework

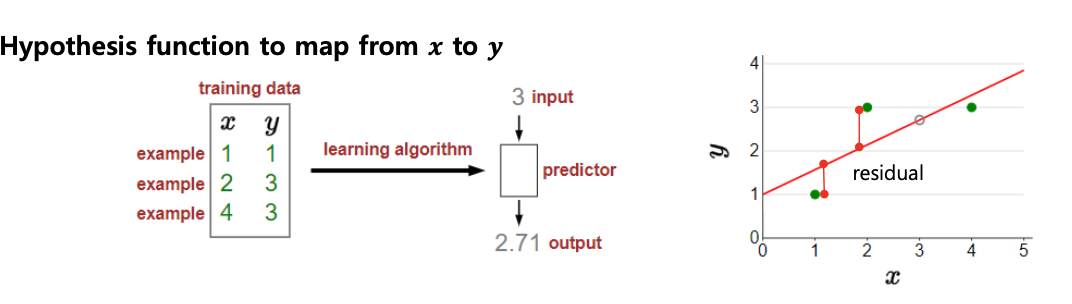
• Linear regression은 주어진 입력에 대해 출력과의 선형적인 관계를 추론하는 문제이다.
• 밑의 그림 처럼 3을 input으로 넣었을 때 에측 결과 2.71 이 나오게 된다.

• Linear regression의 절차
  • 1. 어떤 predictor를 이용할 것인가?
       • Hypothesis class 를 정의해야한다.
       • 위와 같은 경우는 모델 파라미터가 2개이다. (offset, 입력변수 1개)
  • 1. 어떤 손실 함수를 사용해야할까?
       • 보통 선형 회귀 모델에서는 Mean Squared Error(MSE)를 사용한다.
    2. 어떻게 파라미터를 구할까?
       • Gradient descent algorithnm
       • Normal equation

Parameter Optimization

• 앞서 말했듯이 선형 회귀 모델의 경우 동일하게 절차 1,2번을 따른다. 따라서 Linear regression의 3번째 “어떻게 파라미터를 구할까?” 에 대해서 알아보겠다.
• 모델 파라미터가 달라짐에 따라서 주어진 data에 fitting 하는 과정에서 오차가 발생하게 될것이다.

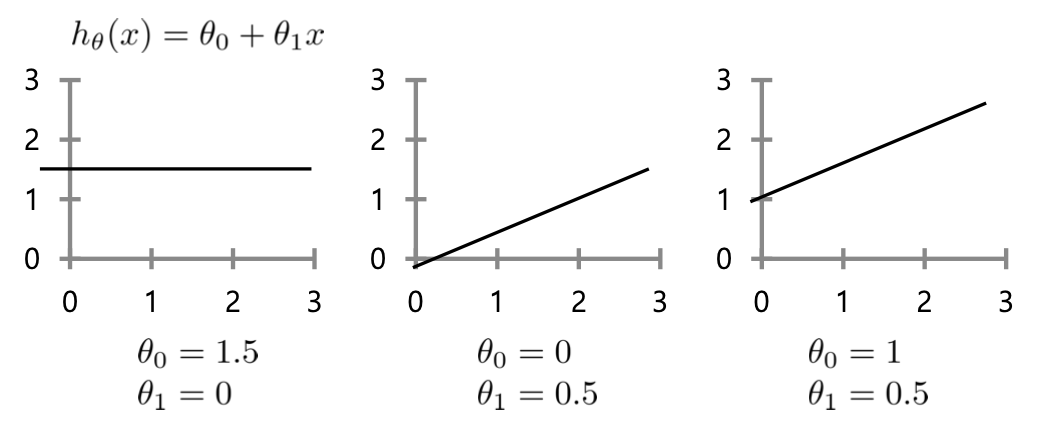
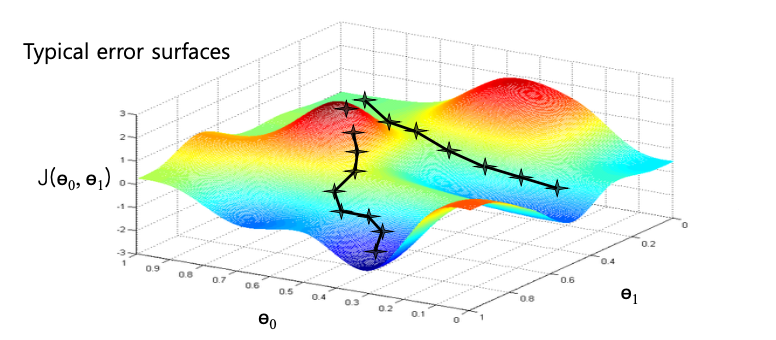
• 다음은 모델 파라미티가 달라짐에 따른 손실함수에 대한 그래프이다.
• 우리의 목적은 이러한 손실함수를 최소화 하도록 하는 모델 파라미터 세타0, 세타1을 구하는 것이다. 그 지점은 그림에서 가장 오목한 부분이다.

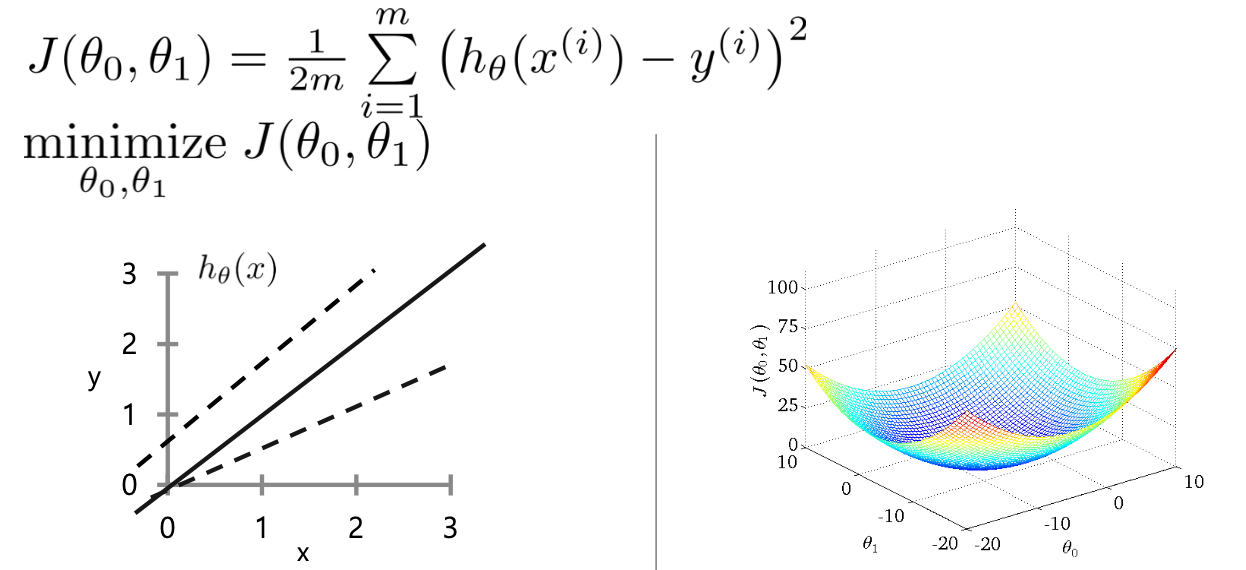
파라미터 최적화

• "”어떻게 파라미터를 구할 수 있을까?” 에 대한 응답이 파라미터 최적화이다.
• 입력데이터를 matrix 형태로 표현한다면 다음과 같다.
• 

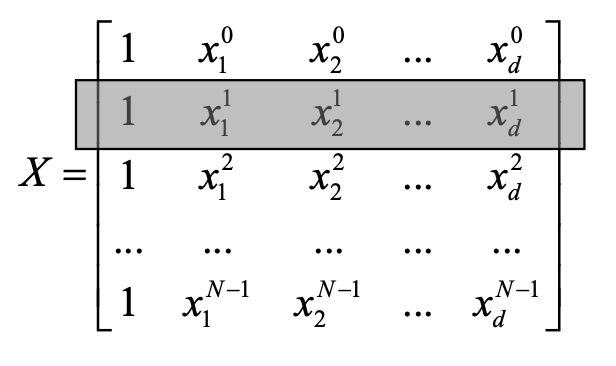
• 세타와 X의 선형 결합을 통해 아래식과 같이 Score을 계산할 수있다.
  • Score값과 Y의 차이를 통해 Loss 를 통한 Matirx를 구할 수 있다.
  • 최적화 파라미터 세타는 이러한 Cost function을 가장 최소화 하는것이다.

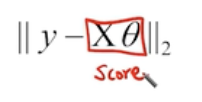
• Soultion:
  • Gradient descent를 통해 iterative(반복적)하게 최적의 파라미터 세타를 찾는다.

Gradient descent(경사 하강법)

• Gradient
  • 함수를 미분하여 얻는 term으로 해당 함수의 변화정도를 표현하는 값
• Gradient decent
  • Gradient 가 0인 지점까지 반복적으로 세타를 바꿔나가면서 탐색을 한다.
    • 해당 지점에서 기울기가 가장 큰 방향으로 간다.

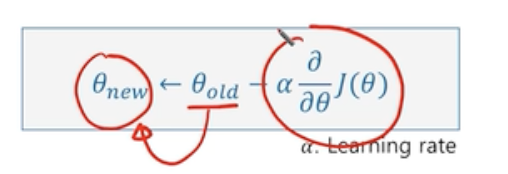
Local optimum VS global optimum

• 지역 최적해(Local Minimum)는 최적화 문제에서 함수가 국부적으로 최소값을 가지는 지점을 나타낸다.

• 경사 하강법과 같은 최적화 알고리즘이 사용되는 경우, 이 알고리즘이 수렴하는 지점이 지역 최적해일 수 있다.

• 지역 최적해는 전체 함수 공간에서 최소값이 아닐 수 있으며, 이는 전역 최적해와 구별된다.

• 경사 하강법 등의 최적화 알고리즘에서는 지역 최적해에 갇히지 않도록 여러 가지 방법이 사용됩니다.
  • 예를 들어, 다양한 초기값에서 출발하여 여러 번의 최적화를 수행하고 결과를 비교하거나,
  • 학습률을 조절하거나,
  • 더 복잡한 최적화 알고리즘을 사용하는 등의 전략이 존재한다.

Quiz

Q. 선형 회귀 분석에서는 입력 특성을 수정하여 솔루션을 해석할 수 있습니다. 점수는 입력 특성과 가중치의 선형 조합으로 계산됩니다. 무게 최종 출력에 대한 입력 기능의 중요성을 설명합니다.

A . 맞습니다.

Q. 선형 회귀에서 가설은 반드시 학습 가능한 매개변수의 선형 형태일 필요는 없습니다.

A. 선형 회귀에서 가설은 꼭 선형 형태일 필요가 없습니다. 입력 특징을 변환하거나 다항식 특징을 추가함으로써 비선형성을 도입할 수 있습니다.

CHAPTER 2. Gradient Descent

Gradient descent algorithm (경사 하강법)

• 우리의 목적은 다음과 같은 손실함수를 최소화하는 파라미터를 찾는 것이다.

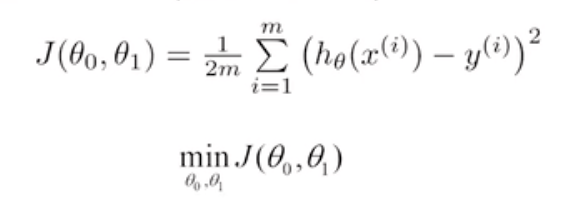
• 이에 대한 방법론으로 Gradient Decent 알고리즘에서는 다음과 같은 outline을 따른다.
  • 1. Initial parameters(초기 파라미터) 세타0, 세타1로 부터 시작한다.
    2. 이 값들을 지속적으로 최소로 하는 지점까지 변화하도록 하는 목적이다.
    3. 함수의 변화량이 가장 큰 (기울기가 가장 큰) 방향으로 파라미터를 업데이트 한다. 이때 step size 는 파라미터 업데이트의 변화 정도를 조정하는 값으로 하이퍼 파라미터 이다.
       • 알파는 사전의 정의된 값이다.
       • 세타는 우리가 구하고자 하는 값이다.

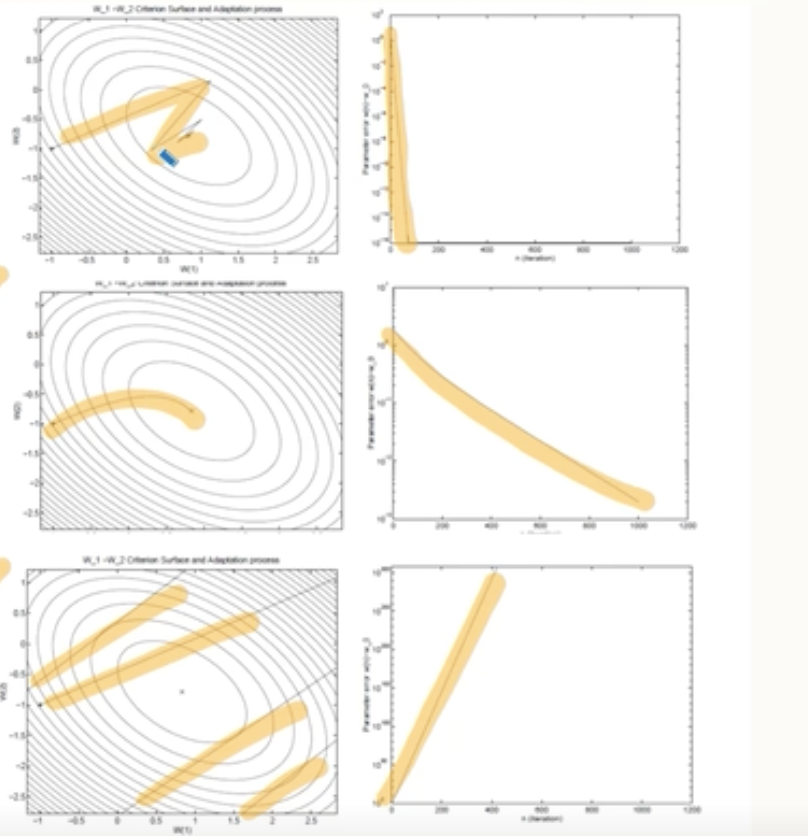
• 다음과 같은 3개의 그래프를 비교해보자.
  • 첫번째 그래프의 경우 알파값에 적당한 경우이다.
    • 어느정도 빠르게 수렴하면서 안정적이다.
  • 두번째 그래프의 경우 알파값이 매우 적은 경우이다.
    • 수렴속도가 굉장히 천천히 떨어진다.
    • 하지만 수렴하는 형태는 굉장히 안정적이다.
  • 세번째 그래프의 경우 알파값이 매우 큰 경우이다.
    • 최소의 지점을 찾기가 어렵고 발산하는 형태이다.
    • Loss또한 오히려 늘어나고 있다.

Batch gradient descent algorithm

• 앞에서와 같은 Gradient desecent algorithm을 Batch gradient descent algorithm라고 표현한다.

• 비록 Local optimum(지역 최적해) 에는 취약하지만, 어느정도 수렴해 가는 것을 알 수 있다.

  

  
  

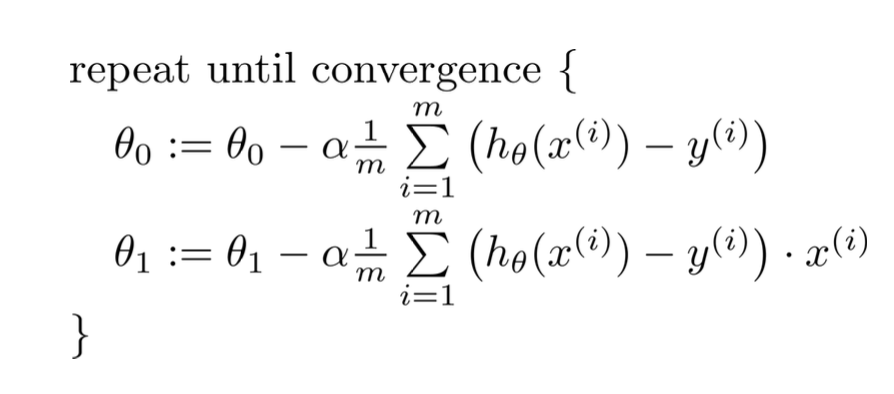
• 하지만 이 알고리즘은 단점이 있다.

  • 위의 수식을 보면 세타를 업데이트 하는 과정에서 전체 샘플 m에 대해 모두다 고려해야한다는 것이다.
  • 이러한 단점을 극복하기 위해서 m을 극단적으로 줄인 알고리즘을 Stochastic Gradient Descent(확률적 경사하강법)라고한다.
    • $SGD : m = 1$
    • 빠르게 iteration을 할 수 있다는 장점이 있지만, 결국 각 샘플에 대해 개별적으로 계산을 하기때문에 noise의 영향이 있다.

Momentum

• 지역 최적해에 취약한 Gradient decent algorithm을 보완하게 위한 알고리즘이다.
• 과거의 Gradient가 업데이트 되어오던 방향 및 속도를 어느정도 반영해서 현재 포인트에서 Gradient가 0이되더라도 계속해서 학습을 진행 할수 있는 동력을 제공하는 것이다.
• Momentum은 현재의 gradient뿐만 아니라 과거의 gradient 업데이트 정보도 고려하여 이전 방향과 속도를 유지하려는 개념이다.

Nesterov Momentum

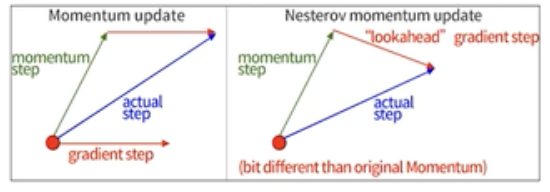
• Momentum update
  • 다음 그림을 보면 현재의 gradient step과 momentum step을 고려해서 actual step (실제 스텝)을 벡터의 합으로써 구한다.
  • 정리하자면 gradient와 momentum으로 actual step을 구한다.
• Nesterov Momentum update
  • 미리 momentum step 만큼 이동한 지점에서 “lookahead” gradient step을 계산하여 이 두개의 스텝으로 actual step을 구한다.
  • 정리하자면 momentum step과 이 미리 예측된 위치에서의 “lookahead” 기울기를 이용하여 actual step을 구한다.

AdaGrad(Adaptive Gradient Descent)

• 각 방향으로의 학습률을 적응적으로 조절하여 학습 효율을 높이는 경사하강법의 알고리즘이다.
• AdaGrad의 수식을 살펴보자
  • 먼저 r은 그래디언트의 제곱이 계속해서 누적으로 더해지기 때문에 r값은 커진다.
  • 또한 r은 파라미터의 분모에 들어가기때문에 델타 세타의 값은 계속해서 작아진다.
  • 이 말은 그래디언트의 누적 값이 커진다는 말은 이미 학습이 많이 진행 되었다는 뜻이기 때문에 델타 세타의 값은 그만큼의 수렴속도를 줄여야하기때문에 작아진다.

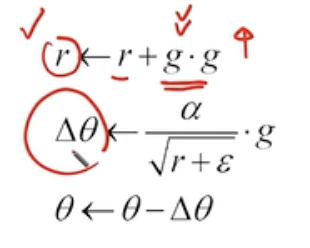
‘학습률이 작아지게 되면 어떻게 되나요?’

• 학습이 일어나지 않게 된다.
  • 이러한 방식을 수정한 것이 RMSProp algorithm이다.

RMSProp algorithm

• 수식에서 볼 수 있다시피 있다시피 RMSProp 방식은 그래디언트의 제곱을 그대로 곱하는게 아니라 기존에 있던 $r$에 ρ(Decay factor는 지수 감소(exponential decay)에서 사용되는 용어) 값을 곱하게 되고 1-p를 그래디언트의 제곱에다가 곱함으로써 과거의 $r$만큼의 p를 곱해서 어느정도 조절하게 된다.

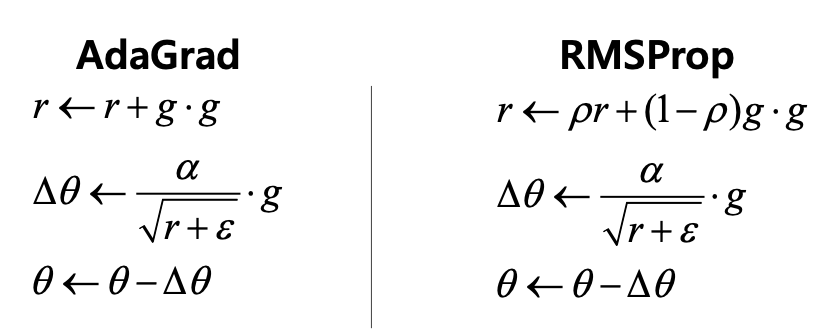
Adam

• 앞으로 머신러닝 또는 딥러닝을 공부 하면서 가장 많이 만나게 될 알고리즘이다.

• Adma은 RMSProp 와 Momentum의 혼합 방식이다.

• 이 알고리즘의 순서는 다음과 같다.

  • 1. 첫번째로 모멘텀을 계산한다. 이 모멘텀은 s와 같은 형태로 구성되어있다.

       $s=p_1⋅s+(1−p_1)⋅g^2$

  • 1. 두번째로는 RMSProp방식으로 두번째 모멘텀을 계산하게 된다.

       $s=p_2⋅s+(1−p_2)⋅g^2$

  • 1. 그다음은 통계적으로 안정된 값을 위해 bias를 Correct 한다.

       

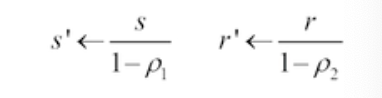
  • 1. 마지막으로 파라미터를 업데이트 한다.

       

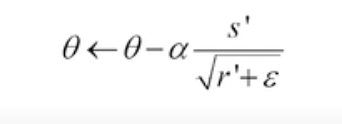
Model 과적합 문제

• model이 지나치게 복잡하여, 학습 파라미터의 숫자가 많아서 제한된 학습 샘플에 너무 과하게 학습이 되는 것이다.
• 입력 feature 의 숫자가 지나치게 많아진다고 하면 항상 좋은것일까?
  • 아니다. 일부 입력변수들은 상호관련 있을수있다.
  • 입력 개수가 많아지면 파라미터가 많아지게 되고 data의 개수 또한 많아진다.
  • 실제 환경에서는 데이터를 충분히 늘릴 수 없는 경우가 있다.
  • 이러한 문제를 해결할 수 있는 대표적 방법은 Regularization방식이다.

Regularizaion(정규화)

• 복잡한 모델을 사용하더라도 학습 과정에서 모델의 복잡도에 대한 패널티를 줘서 모델이 오버피팅 되지 않도록 하는 방식이다.

• 수식을 살펴보면 MSE 부분을 fitting이라고 한다면 그 뒤의 수식은 세타 j값이 크면 클수록 늘어나게 되는 오류이다.

  • 모델의 입장에서는 가능한한 세타를 쓰지 않으면서 이 Loss 를 최소화하는 노력을 한다.

    

  • 이 정규화 항은 가중치가 커질수록 전체 손실 함수를 증가시키므로, 모델은 가중치를 작게 유지하려고 노력하게 된다. 이는 모델이 더 간단한 형태로 학습되도록 유도하여 오버피팅을 방지하는 역할을 한다.