[LG Aimers] 4-2. Supervised learning (classification/regression)

24-01-12 9 분 소요

[공지사항] [해당 내용은 LG에서 주관하는 LG Amiers : AI 전문가 과정 4기 교육 과정입니다.] 강의를 듣고 이해한 내용을 바탕으로 직접 필기한 내용입니다. LG AI

4-2. 지도학습(분류/회귀)

교수 : 이화여자대학교 강제원 교수
학습목표
- Machine Learning의 한 부류인 지도학습(Supervised Learning)에 대한 기본 개념과 regression/classifiation의 목적 및 차이점에 대해 이해하고, 다양한 모델 및 방법론을 통해 언제 어떤 모델을 사용해야 하는지, 왜 사용하는지, 모델 성능을 향상시키는 방법을 학습하게 됩니다.

CHAPTER 3. Linear classification

Linear Classification

Linear regression 모델과 같이 다음과 같은 수식을 따른다.
입력 freature x 와 그에 해당하는 파라미터셋 w 의 내적으로 구성되어있다.
- 예측=x⋅w+b
가설 함수(hypothesis function)가 선형이라고 가정할 때, 이 함수의 결정 경계(decision boundary)는 데이터를 분리하는 초평면(hyperplane)이 된다.
- 가설 함수 h(x)가 0보다 크면 양성 클래스(positive class), 0보다 작으면 음성 클래스(negative class)로 예측한다고 가정하면, 결정 경계는 가설 함수가 0이 되는 부분이다.
- 결국 우리의 목적은 이러한 hyper plane을 구해서 우리의 data set에 있는 positive class 와 negetive class를 구분하는 것이다.

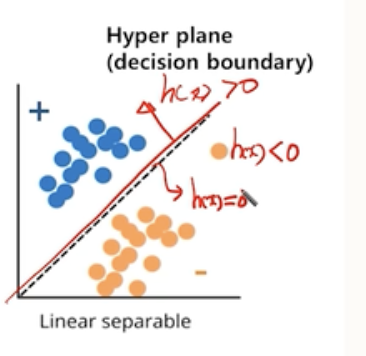
Linear model 이 갖는 여러 장점 즉, 단순하며 해석 가능성이 있고 다양한 환경에서 일반적으로 안정적인 성능을 제공할 수가 있다.

Linear classification framework

밑의 그림처럼 우리는 h(x)에 대하여 (2,0)이 들어갔을때 -1이 출력 될 것을 기대한다면 다음과 같은 과정을 따른다.

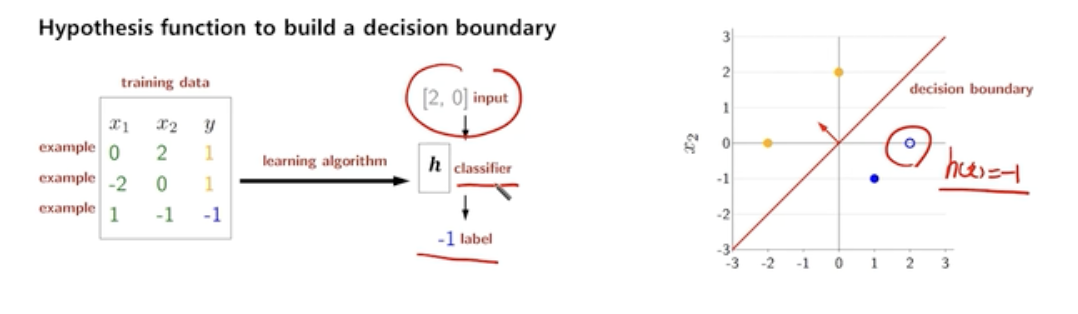
Linear classification의 절차
- 1. 어떠한 예측 변수를 사용할것인가?
- 1. 어떠한 손실 함수를 설정 할 것인가?
    - Linear regression의 경우 MSE를 사용하지만
    - Linear galssification의 경우 Zero-one loss, Hinge loss, Cross-entropy loss를 사용한다.
- 1. 어떻게 파라미터를 최적화 할까?
  - Gradient decent algorithm을 사용한다.

Linear classification model

$h(x) = w_0 + w_1x_1+w_2x_2+w_2x_2$
- 먼저 입력 변수와 파라미터의 곱으로 score를 계산한다. 이때 $w0$는 offset 이다.
  - offset이란 상수항이다. 회귀 모델이 독립 변수가 0일 때의 기본값을 나타낸다.
score 값을 계산 한 이후에는 그 출력에 sign함수를 적용하게 된다.

h(x)가 0보다 큰 구역, 작은 구역을 정의 하게 되는데, x가 0보다 크면 sign 함수에 의해 1, x가 0보다 작으면 -1 이 된다.

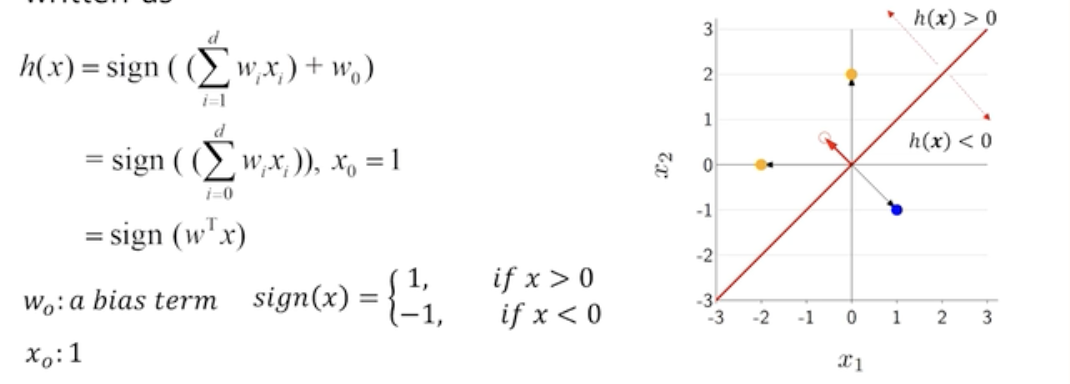
Hypothesis class : which clssifier?

우리의 목적으로 되돌아와보자면 우리의 문제는 parameter w를 학습하는 것이다. w가 바뀜에 따라 샘플들의 판별 결과 또한 바뀌게 된다.
다음 수식 처럼 sign함수에 따른 결과가 바뀌게 되면 positive sample과 negetive sample의 결과가 뒤바뀌게 된다.

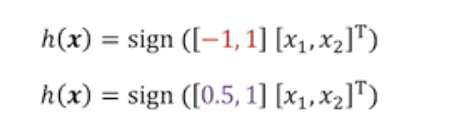
그렇다면 Classification 문제에서 어떻게 Error를 판별할 수 있을까?

하나의 예시로 Zero-One Loss를 생각 할 수 있다.
- 이 losss는 내부의 logic을 판별하여 맞으면 0 틀리면 1을 출력하는 함수이다.

Zero-One Loss

Zero-One Loss 는 내부의 logic을 판별하여 맞으면 0 틀리면 1을 출력하는 함수이다.
$Loss([0,2],1,[0.5,1]) = 1[sign([0.5,1] * [0,2]) != 1] = 0$
- 다음 수식을 살펴보자, $Loss([0,2],1,[0.5,1]) = 1$ 이 부분이 Zero- One Loss function이다. 하지만 내부의 값 둘을 내적한 것이 1이 아님을 알게 된다. $[0.5,1] * [0,2]) != 1$ 이다.
- 따라서 false, 0이 된다.
하지만 Zero-One Loss는 불연속성과 미분 불가능성 때문에 경사 하강법과 같은 최적화 알고리즘에서 사용하기 어려울 수 있다. 이러한 문제를 해결하기 위하여 classification에서 hinge Loss 를 사용한다.

Hinge Loss

각 샘플에 대해 모델의 예측과 실제 레이블 간의 여유(margin)를 고려하는 분류 모델에서 사용되는 손실 함수 중 하나이다. 다음 수식을 살펴보자
$Hinge Loss(w,b,x_i,y_i)=max(0,1−y_i⋅(w⋅x_i+b))$
w는 가중치(weight) 벡터,
b는 편향(bias),
xi는 입력 데이터의 특성(feature) 벡터,
yi*는 실제 레이블,
$y_i(w⋅x_i+b)$는 모델의 예측과 실제 레이블 간의 여유(margin)를 나타낸다.
이 수식에서는 0과 margin 사이의 max 값을 찾는 Loss이다. margin이 1보다 작으면 max값을 통해 손실 함수를 갖게 되고 margin이 1보다 크면 음수값이므로 max값은 0을 선택하게 되어 Loss는 0이된다.
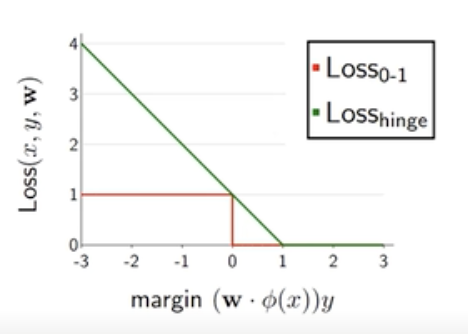
결론적으로 margin이 크면 손실이 0이된다.

Cross-entropy Loss

Cross-entropy Loss는 Classification모델에서 가장 많이 사용되는 손실 함수이다.
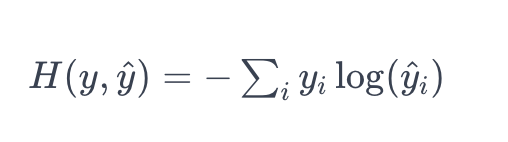
- y는 실제 레이블의 확률 분포이다. (예: 실제로 고양이인 경우 [0, 1])
- y^는 모델의 예측 확률 분포이다. (예: 모델이 고양이라고 예측한 경우 [0.2, 0.8])
즉, 크로스 엔트로피는 두 확률 분포 간의 “차이”를 측정하는데, 이 거리가 작을수록 모델의 예측이 좋다고 판단된다. 이 학습의 목표는 이 크로스 엔트로피를 최소화하여 모델을 더 정확하게 만드는 것이다.

Sigmoid

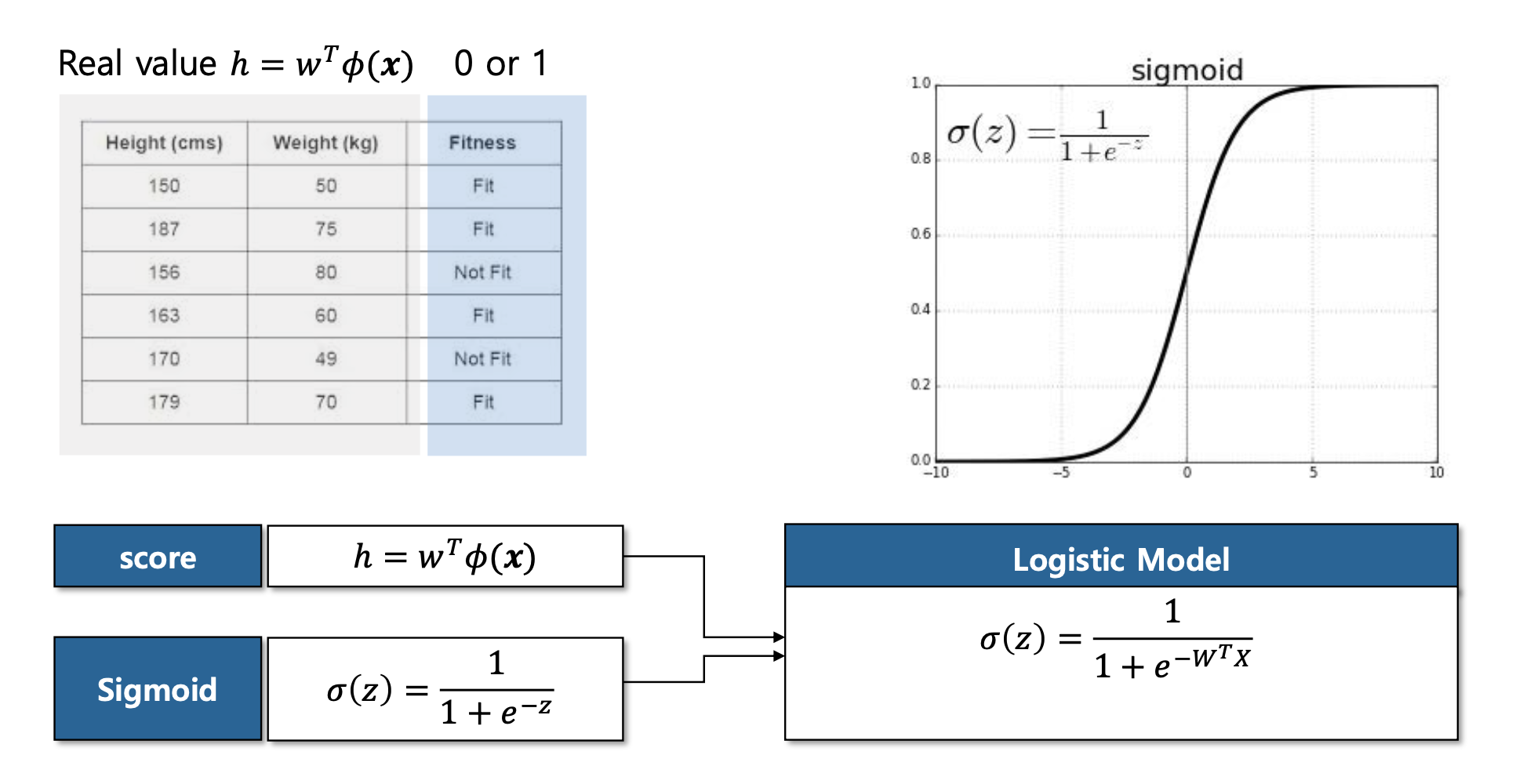
시그모이드 함수를 이용하면 score값을 매핑 할 수가 있다.
밑의 슬라이드를 보면 쉽게 이해가 된다.
- sigmoid함수에 따라 +방향으로 증가하게 된다면 1에 근사하게 되고 -방향으로 간다면 0에 근사하게 된다. 0에 근사하게 된다면 1/2 값을 갖게 된다.
- Score 실수값을 0부터 1사이의 값으로 매핑 할 수가 있는데 이를 로지스틱 모델이라고 한다.

Multiclass classification

Binary classification 문제를 Multiclass classification 문제로 확장 할 수가 있다. 이것을 One-VS-All 방식으로 이해 할 수가 있다.
그림에서 볼 수 있듯이 3개의 Hyper plane을 그어서 Multiclass classification문제를 Binary classification문제로 풀 수 있게끔 할 수 있다.

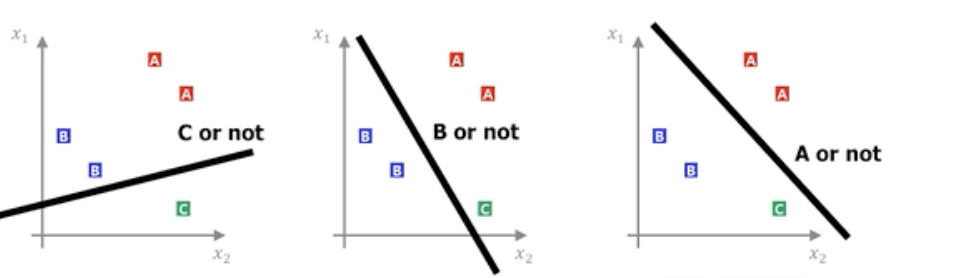
A or not 에 대한 파라미터부터 C or not에 대한 파라미터까지 벡터로 정의한다면 다음과 같이 Score값의 형태가 나온다.
- 이렇게 얻게된 Score값들에 시그모이드 함수를 사용하게되면 확률값으로 매핑할 수가 있게 된다.

CHAPTER 4. Advanced Classification

Margin

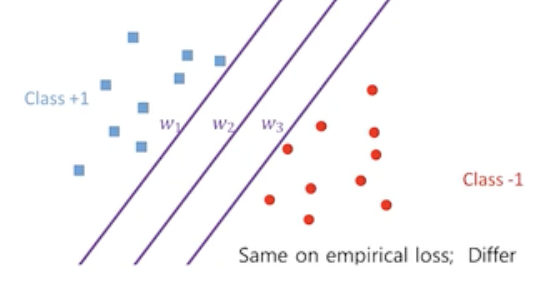
다음과 같은 그림에서 Hyper plane을 어떻게 긋느냐에 따라 new data의 분류가 정해지게 되며 성능 또한 달라진다.
이러한 문제를 해결 하는 방법은 SVM에서 중요한 Margin이라는 개념이다.

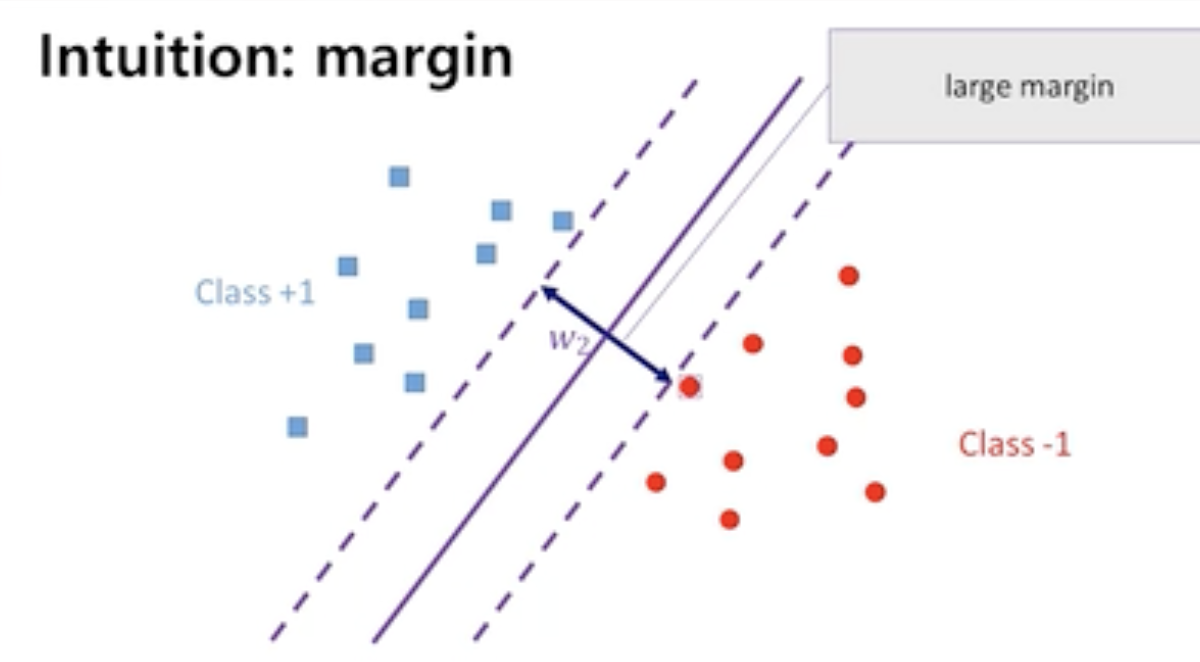
그림에서와 같이 hyper plane과 가장 가까운 positive sample과 negetive sample을 기준으로 점선을 긋는다.
Hyper plane과 이 둘 점선의 위치가 가장 동일한 구간이 최대 margin을 확보할 수있는 최적화 방식이다.

Support Vector Machine

서포트 벡터 머신에서는 이러한 개념을 설명하기 위해서 서포트 벡터라는 것을 정의하게 된다.
- 서프트 벡터는 positive, negetive sample 중에서 hyper plane과 가장 가까운 sample을 뜻한다.
- 이 것은 성능을 결정하는 가장 중요한 Data Point이다.
- SVM의 목표는 이 마진을 최대화하는 결정 경계를 찾는 것이다.
Support Vector Machine에서는 다양한 최적화 방법을 사용한다.
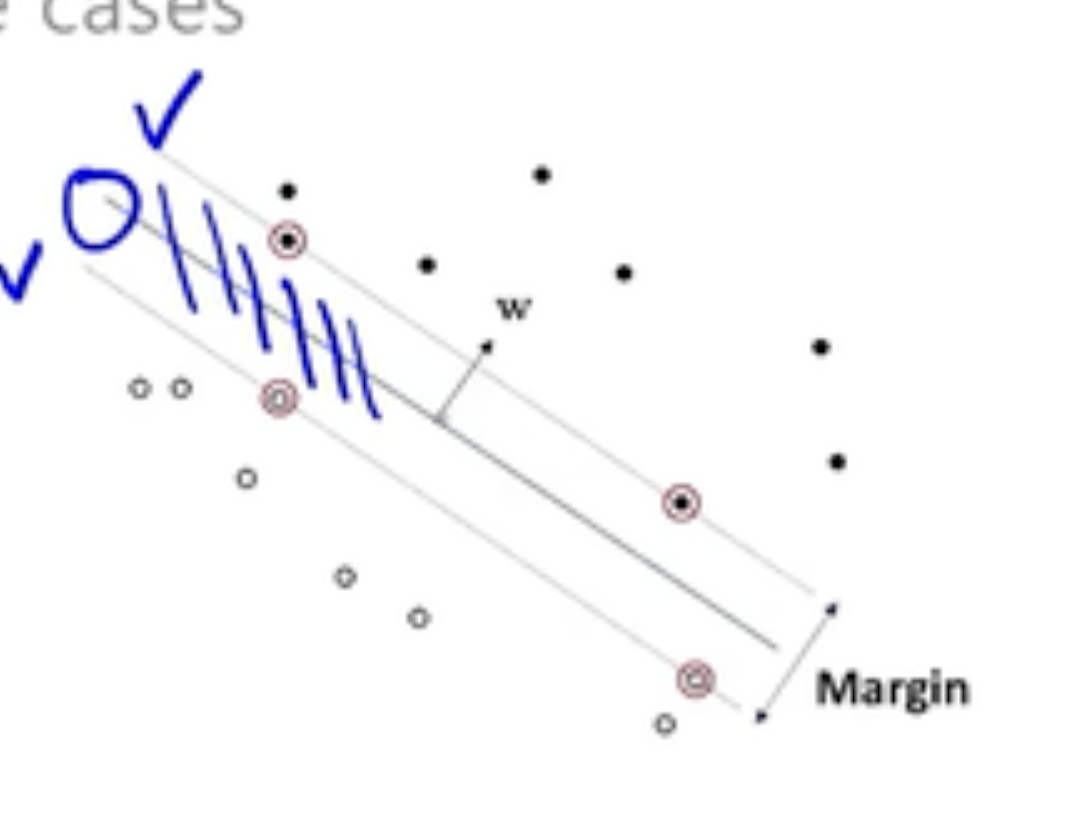
- Hard margin SVM
  - 그림과 같이 Hyper plane과 서포트 벡터 사이의 공간에 어떠한 sample도 존재하지않는다.
- Soft margin SVM
  - hard margin SVM과 달리 어느 정도의 error를 용인한다.
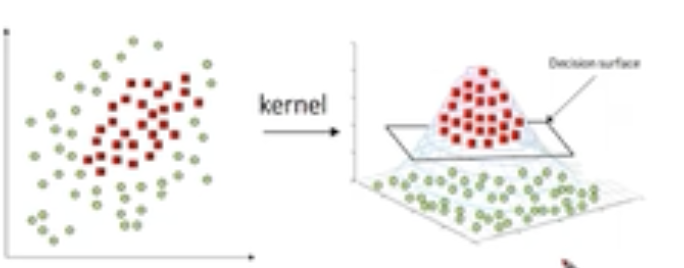
- Nonlinear transform & kernel trick
  - SVM의 Linear한 환경에서 사용할 수 있다는 단점을 극복하기 위해 만들어졌다.
  - 2차원의 sample을 좀 더 고차원으로 맵핑하는 함수를 이용한다.

Hard Margin SVM

가설함수 h(x)가 0이 되는 부분이 Hyper plane이다.
계산상의 편의를 위해 서포트 벡터들이 갖는 값을 각각 +1, -1이라고 생각해보자
- 그렇다면 다른 samle들은 Positive의 경우 1보다 크고, Negetive의 경우 1보다 작게 된다.
- 최종적으로 $y$와$(w^Tx+b)$를 곱하면 모든 샘플에 대해서 1보다 크거나 같은 경우가 나온다.
- 이를 SVM에서의 Constraint(제약조건)이라고 말하게 된다.

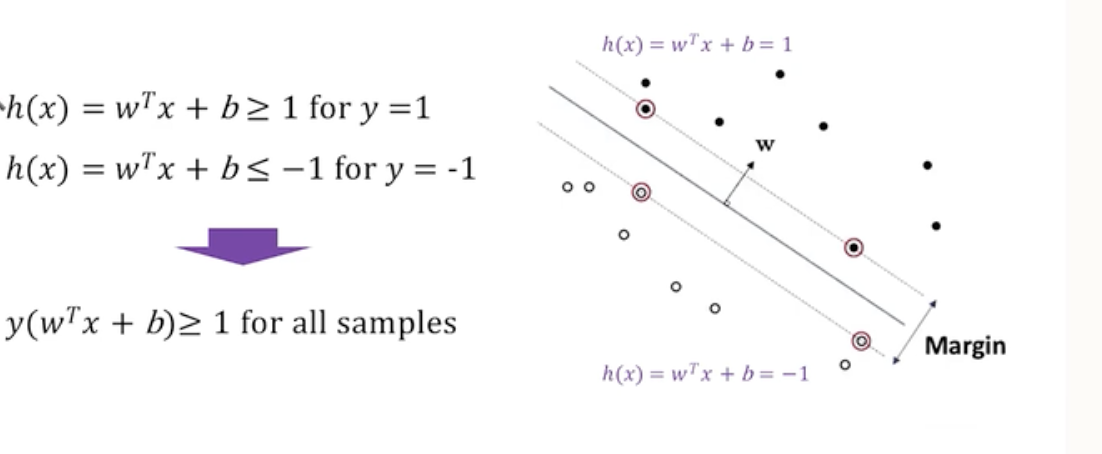
다시 Margin으로 돌아와서 마진은 SVM에서 다음과 같다.

positive와 negetive의 거리가 같기 때문에 *2/

* 를 최대화 하는 것이 목표이다.

이 말은 즉 *

* 를 최소화 하는 것과 똑같은 말이다.

SVM Primal problem

norm w는 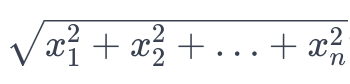과 같은 수식을 따른다. 그렇게 때문에 편의를 위해 제곱을 하고 결론적으로는 이를 제곱한것에 최소화하는 것과 동일하다고 말할 수 있다.
또한 위에서 말했듯이 제약조건 $y(w^Tx+b)>=1$ , 이 두가지가 SVM의 Primal problem이다.!!

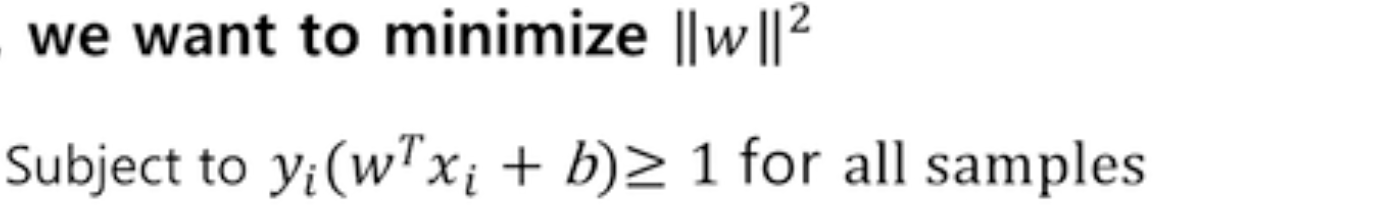
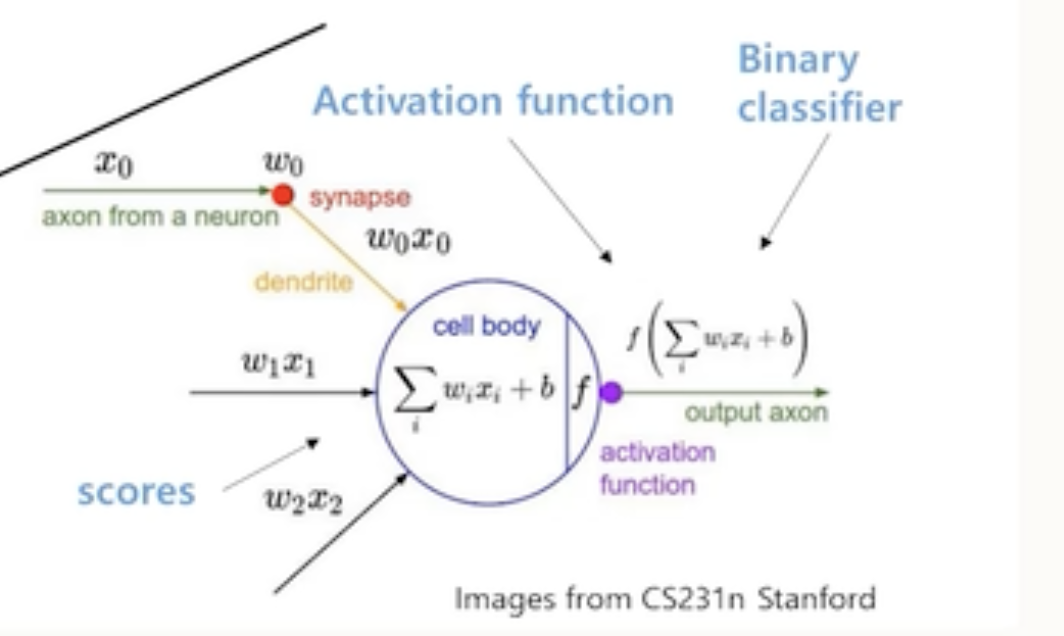
ANN(Arifical neural network)

Non-linear classification model
ANN 또한 다음 그림에서 볼 수 있다시피 x와 파라미터의 선형결합을 통해 구한 Score값을 이용하게 된다. 하지만 ANN은 Non-linear한 구조를 가지고 있다. 그러한 연산이 Activation function에 의해서 이뤄지게 된다.
Score값을 Activation function의 입력으로 쓰면서 시그모이드와 함수와 같이 non-linear한 맵핑한 결과 만들어 내게 된다.

Activation functions

초기에는 시그모이드 함수를 사용했지만, 깊이있는 학습에 도움이 되지 않는다고 알려져있다.
따라서 ReLU와 같은 함수를 이용한다.
왼쪽의 시그모이드 함수의 경우 z값이 매우 커지거나 작아짐에 따라서 그래디언트가 굉장히 작아지게 되어서 학습이 진행됨에 따라 학습량이 점차 줄어드는 단점이 있다.
- 따라서 그래디언트 값이 1로 유지되는 ReLU가 가장 많이 활용된다.

Multilayer perceptron model (MLP)

Neural Network를 여러 개의 층으로 쌓은 것을 의미한다.

For Example : XOR

XOR 문제는 어떠한 하나의 Hyper plane을 그어도 효과적으로 분류 할 수 없게 된다. 그럼 어떻게 해결할 수 있을까?

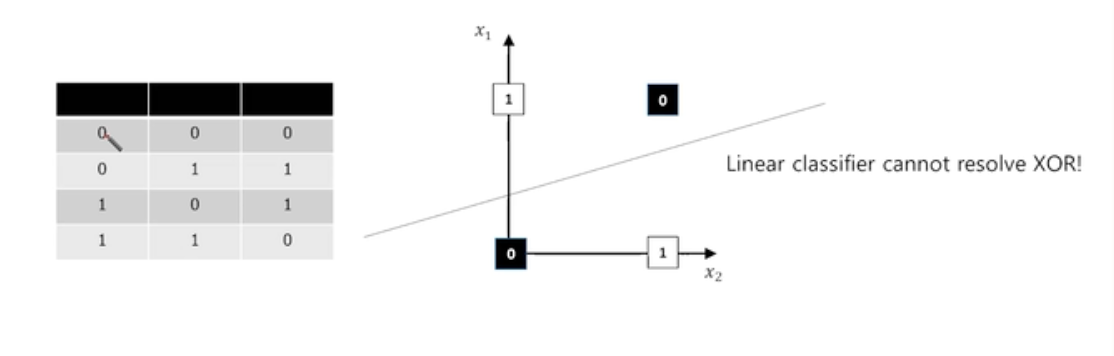
다음 슬라이드를 보면 쉽게 이해할 수 있다.
- (x1, x2)가 (0,0) 이라고 할때, w와 b가 나타나있으므로 각각 y1,y2를 구할 수가 있다.
- y1,y2를 입력으로 넣고 출력을 구하게 되면 시그모이드 함수를 통해 XOR문제를 쉽게 구할 수가 있다.

최종적으로 구한 답이다.

CHAPTER 5. Ensemble

Ensemble Learning

Ensemble Learning은 이미 사용하고 있거나 개발한 알고리즘의 간단한 확장이다.
Supervised learning task에서 성능을 올릴 수 있는 방법이다.
머신러닝에서 알고리즘의 종류에. 상관 없이 서로 다르거나, 같은 매커니즘으로 동작하는 다양한 머신러닝 모델을 묶어 함께 사용하는 방식이다.
예를 들어, SVM, Neural Network Model과 같이 여러 다른 model을 함께 모와서 예측 model의 집합으로 사용하는 것이다.

Ensemble Methods

앙상블 모델의 학습 과정은 다음과 같다.
- 학습 데이터 S를 랜덤하게 S1부터 Sn까지 나누어서 학습을 진행한다.
- 이러한 앙상블은 서로 다른 모델로 구성할 수 있지만 같은 학습 모델로 구성 될 수 있다.
- 최종 결정은 마지막에 학습한 다수의 모델이 각각 결정을 내린후에 다수결로 예측 결과를 제공한다.

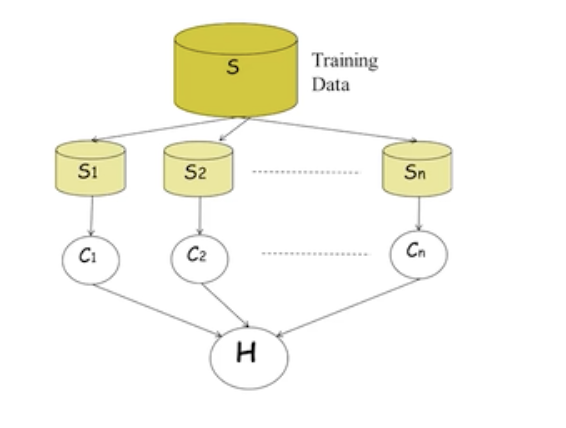
앙상블을 구성하는 기본적인 요소 기술은 bagging 과 boosting의 개념이 있다.
앙상블 기술의 장점은 예측 성능을 안정적으로 향상시킬 수 있다는 것이다.
- 다양한 모델의 결정으로 최종 예측결과를 제공하기 때문에 noise등에서 보다 안정적이다.
- 다양한 모델을 사용하고 직접적으로 연합하여 적용하기 때문에 쉽게 구현이 가능하다.
  - 각 모델이 독립적으로 사용되기 때문에 모델 파라미터의 튜닝이 많이 필요없다.
앙상블 기술의 단점은 모델 자체로 간결한 표현이 되기 어려운 문제가 있다.

Bagging

Bagging은 학습 과정에서 training sample을 랜덤하게 나누어 선택해 학습하는 것이다.
학습데이터 S를 N개로 구분하여 서로다른 Subset을 구성하여 서로 다른 Classifier을 사용한다.
- 설령 같은 모델을 사용하더라도 Random한 Subset을 이용하기 때문에 다른 특성을 갖게 된다.
각 Sample set이 다른 모델에 영향을 끼치지 않기 때문에 모델을 병렬적으로 학습하게된다.

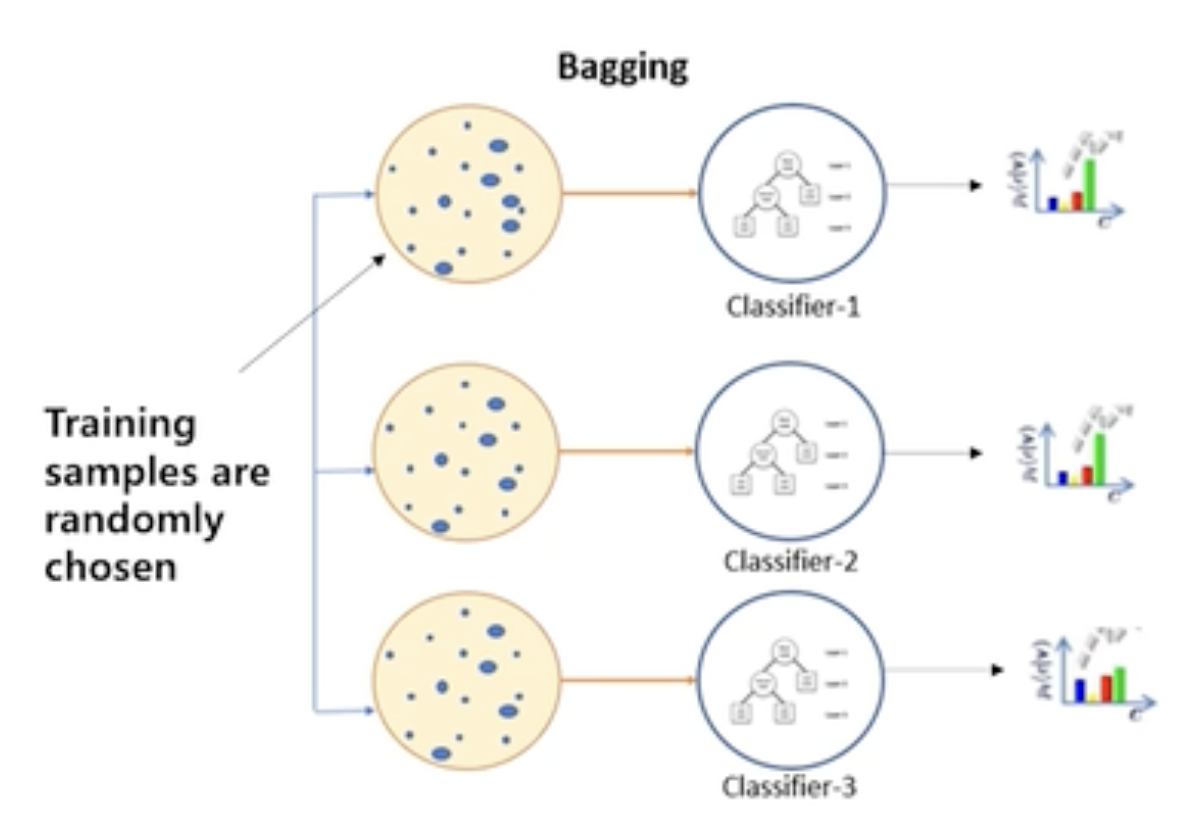
Bagging의 장점
- 오버피팅 감소
  - Training sample의 숫자가 적거나 반대로 모델이 복잡한 경우에 발생하는 오버피팅 문제에 대해 각 샘플을 병렬적으로 사용하기 때문에 성능이 좋다.
- 분산감소
  - 각 모델이 독립적으로 학습되기 때문에, Bagging은 전체 모델의 분산을 감소시킨다. 따라서 일반화 능력이 향상된다.

Boosting

Bagging하고 다르게 순차적으로 동작한다.
밑의 그림에서 볼 수 있다시피 먼저 Classifier-1을 통해서 예측을 수행한다.
- 이때 Classifier-1의 결과인 샘플의 중요도인 weights를 다음 학습에 쓰게된다.
- 이전 Classifier의 결과를 현재 Classifier의 결과를 향상하는데 사용하게 된다.

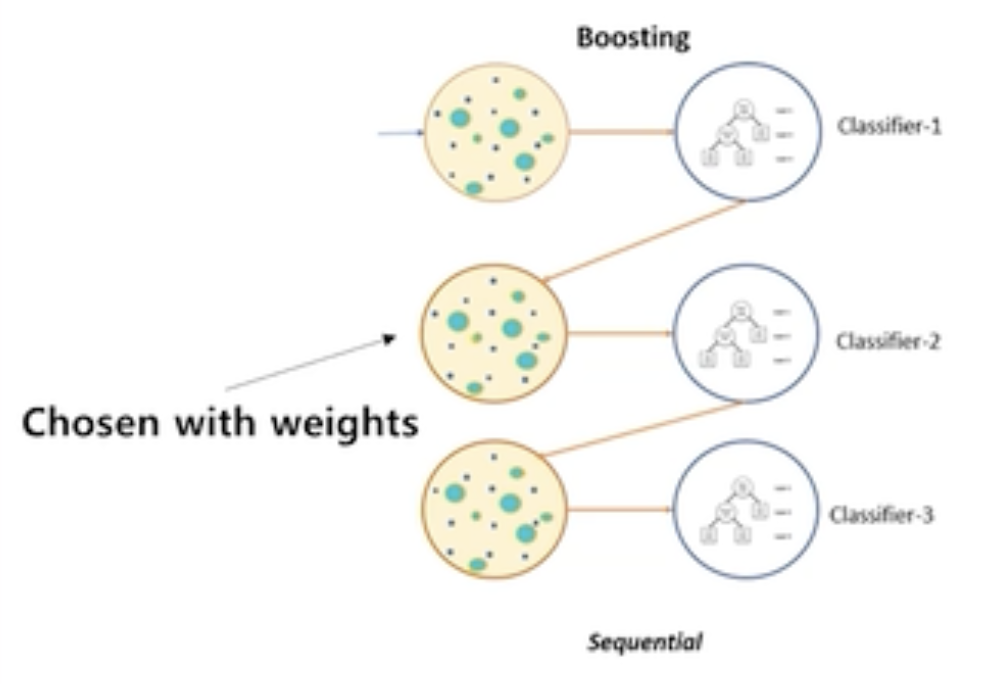
Weak Classifier의 Cascading
- Cascading은 Boosting의 한 형태로, 성능이 낮은 Weak Classifier들을 순차적으로 결합하여 성능을 향상시키는 방법이다,
- 그렇다면 Weak Classifier란 뭘까?
  - Bias가 높은 Classifier를 뜻한다.
  - 모델 자체가 단순해서 즉 Strong Classifier에 비해 성능이 낮아서 혼자서는 무엇을 하기 어려운 모델이다.
- 그렇다면 Cascading은 무엇일까?
  - Weak Classifier를 순차적으로 학습하고 예측하여 모델의 성능을 향상시킨다.
  - 첫 번째 Classifier로 예측 후, 틀린 부분 집합에 대해 다음 Classifier를 학습하고 예측한다.
- 이러한 Weak Classifier를 Cascading을 하면 연속적으로 Classifier의 성능을 높일 수 있다.
- 그림에서 볼 수 있다시피 단순한 모델을 선형적으로 학습을 하여 Classifier의 성능을 높이게 된다.

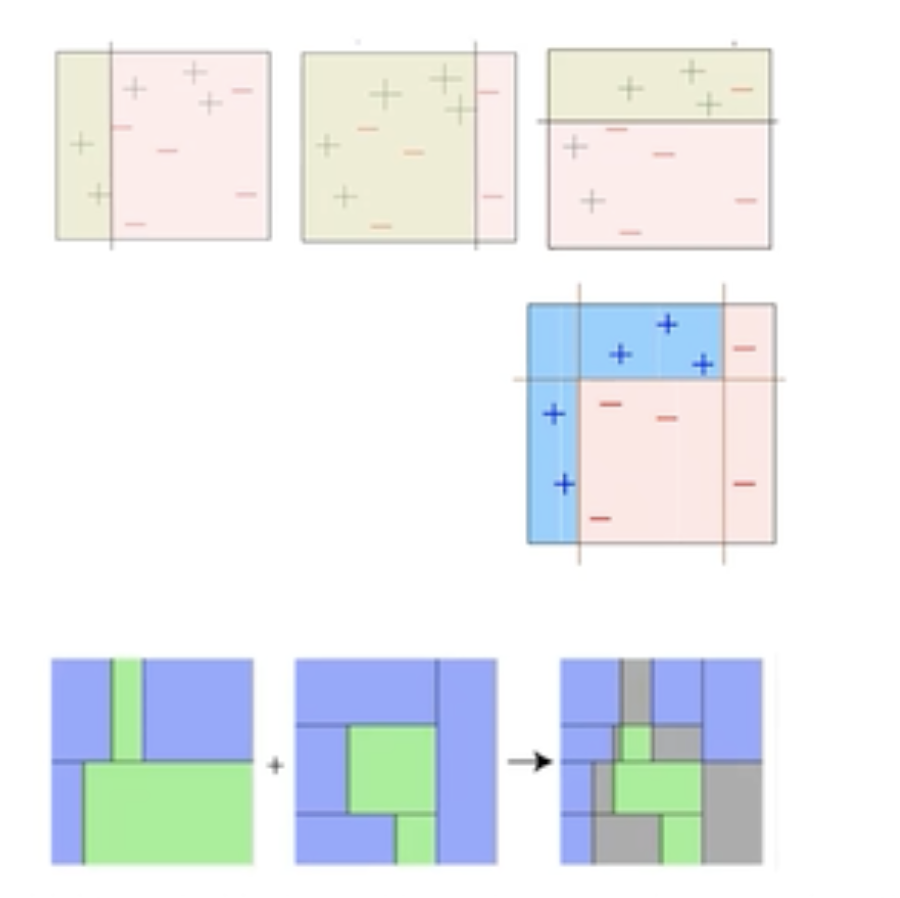
Adaboost

대표적인 Boosting 알고리즘으로 Adaboost를 뽑을 수 있다.
Adaboost는 base classifier에 의해서 오분류된 sample에 의해 보다 높은 가중치를 두어 다음 학습에 사용할 수 있다.
이런방식의 장점은 간단하게 구현이 가능하며 특정한 학습 알고리즘에 구애받지 않는다는 점이다.
그림에서 볼 수있는 것처럼 오분류된 sample에 높은 가중치를 두어 다음 Classifier는 어려운 error를 해결하는데 특화된 모델로 동작하게 된다.
- 이러한 연속적인 Classifier의 동작으로 최종적으로 우수한 결과를 제공한다.

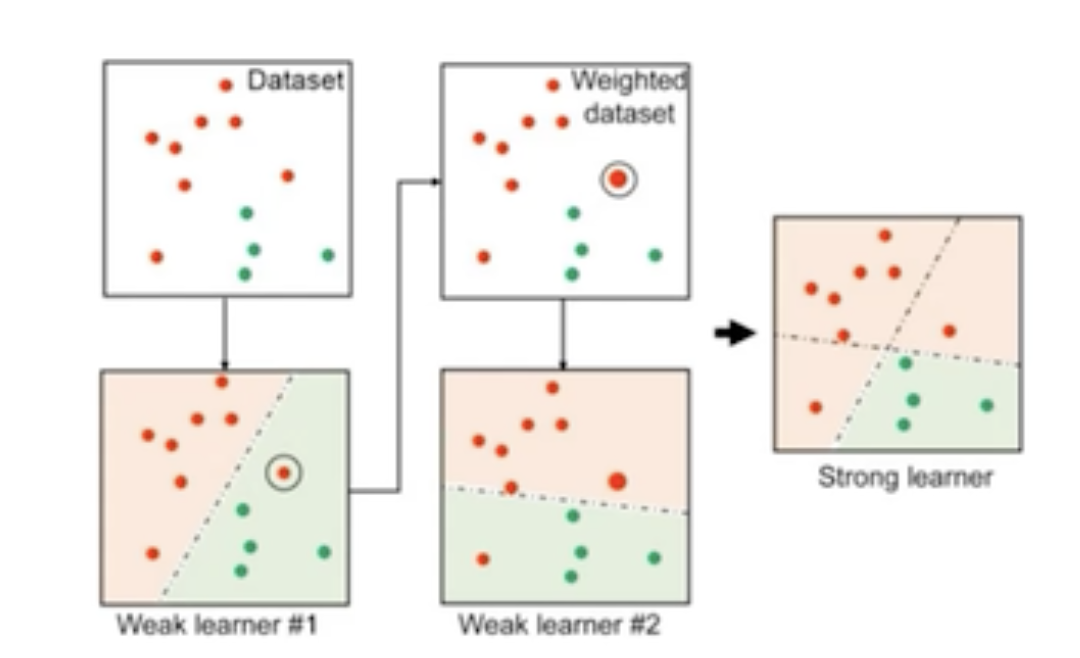
Random Forest

Bagging과 Boosting을 활용한 대표적인 알고리즘으로 Random Forest모델을 뽑을 수 있다.
Random Forest는 decision tree의 집합이다.
Bagging
- 서로 다르게 학습된 decision tree의 결정으로 예측이 수행되기 때문에 자체적으로 bagging을 통해 학습한다.
- 다양성을 증가시키기 위해 서로 다른 데이터 부분집합에 대해 트리를 학습한다는 말이다.
Boosting
- 매 노드에서 결정이 이뤄지기 때문에 자체적으로 Boosting을 실행한다.
- 대표적으로 gradient boosting machine(GBM) 방식이 유명하다.

모델 성능 평가

Accuracy(정확도)
- 정확도는 모델이 전체 데이터에서 얼마나 맞추었는지를 나타내는 지표이다.
confusion matrix (혼동행렬)
- 혼동 행렬은 모델이 각각의 클래스를 어떻게 예측했는지를 보여주는 표이다.
  - True Positive (TP): 양성으로 예측했는데 맞춘 경우
  - True Negative (TN): 음성으로 예측했는데 맞춘 경우
  - False Positive (FP): 양성으로 예측했는데 틀린 경우 (실제는 음성)
  - False Negative (FN): 음성으로 예측했는데 틀린 경우 (실제는 양성)
다음 표를 살펴보면 조금 더 이해하기가 쉽다.
- 혼동행렬을 통해 Accuracy, F1 Precision, Recall등을 구할 수 있다.
Unbalanced 데이터 세트의 경우 accuracy(정확도)이외에도 Precision(정밀도), Recall(재현율), F1(정밀도와 재현율의 조화평균) 등을 동시에 보아야 모델 성능을 제대로 측정 할 수 있다.

ROC Curve

서로 다른 Classifier의 성능을 측정하는데 사용하는 곡선이다.
TPR(True positive Rates), TNR(Ture negetive Rates)
가로축은 FPR인데 이는 1에서 TPR값을 뺀 값이다. 세로축은 Recall값을 의미한다.
- 왼쪽 상단으로 갈 수록 성능이 좋다고 할 수 있다.

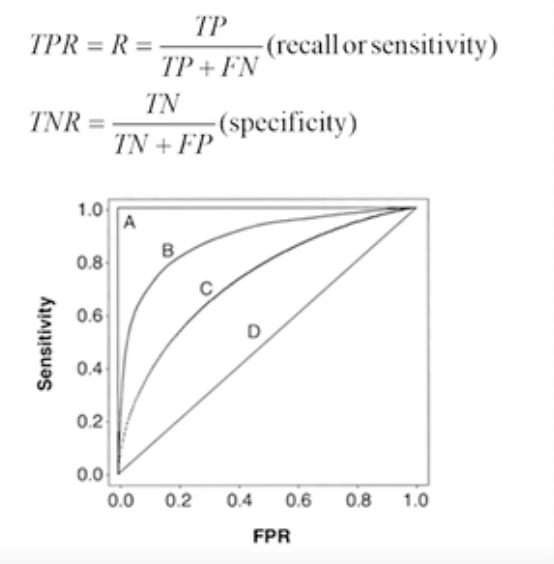
모델의 설명력에 맞게 각 성능 지표의 중요성을 모델마다 잘 판단해야한다.

Applications using SL

R-CNN (Region-based Convolutional Neural Network)
- SL을 사용하는 딥러닝 모델이다
  - R-CNN은 Selective Search (SL)라고 불리는 객체 후보 영역을 찾는 기술을 사용한다. SL은 이미지에서 가능성 있는 객체의 위치를 추정하여 이들 위치를 후보로 선택하는 방식이다.

CNN, LSTM등은 SL의 대표적인 예시이다.
- 이 모델들은 훈련 데이터셋이 주어진 상태에서 입력과 출력 간의 관계를 학습합니다. CNN은 이미지 분류와 같은 작업에서 사용되고, LSTM은 시퀀스 데이터 처리에 적합하다.
Semantic segmentation(의미적 분할)
- 자율주행 task이다.
- 영상을 구성하는 pixel에 대한 classification 문제이다.
Face recognition(얼굴 인식)
Face detection(얼굴 감지)
Super resolution(고해상도화)

Twitter Facebook LinkedIn