4 분 소요

[공지사항] [해당 내용은 LG에서 주관하는 LG Amiers : AI 전문가 과정 4기 교육 과정입니다.] 강의를 듣고 이해한 내용을 바탕으로 직접 필기한 내용입니다. LG AI



5-1. 딥러닝(Deep Learning)

  • 교수 : KAIST 주재걸 교수
  • 학습목표
    • Neural Networks의 한 종류인 딥러닝(Deep Learning)에 대한 기본 개념과 대표적인 모형들의 학습원리를 배우게 됩니다.
    • 이미지와 언어모델 학습을 위한 딥러닝 모델과 학습원리를 배우게 됩니다.



CHAPTER 1. Introduction to Deep Neural Network



심층 신경망 (deep neural netwoks)의 기본 동작 과정

  • 딥러닝
    • 신경세포들이 여러 지능적인 task를 수행 수 있도록 신체 내에 두뇌의 동작 과정을 모방해서 수학적인 알고리즘을 만든것을 딥러닝 알고리즘이라고 한다.
  • 인공지능 < 머신러닝 < 딥러닝
    • Data에 대해서 입력과 출력의 관계를 모방하고 본따 새로운 입력이 주어졌을 때 task를 잘 수행하도록 ㅎ나는것이 머신러닝이다.
    • 두뇌속 신경세포들의 망 과정을 본따서 만든 기계학습의 일종이 딥런이이다.
    • 최근 컴퓨터비전 , 자연어처리 등에 좋은 성능을 내고 있다.
  • 신경세포 하나는 다른 신경세포와 연결 되어 있고, 다른 신경 세포들로부터 넘어온 전기신호를 신경 세포 하나에서 나름의 변화된 전기신호를 만들어내고 신경세포가 연결되어있는 다른 신경세포에 전달한다.
    • 해당 과정을 수학적인 알고리즘으로 정의하면 다음과 같다.
    • 신경 세포 하나를 x1부터 x2 … 으로 정의하게 된다.
    • 해당 신경세포는 가중치를 곱하고 상수항까지 더한 1차결합식으로 새로운 신호를 만들어낸다.
    • 추가적으로 활성화 함수를 통과해서 최종 output을 만들어낸다.

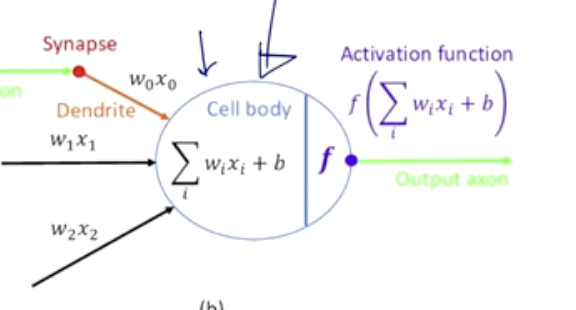
image-20240117161724073

  • Deep Neural Network
    • 정보 처리 단계를 몇단계가 아니라 수십 혹은 수백 단계에 걸쳐 정보를 처리함으로써 고수준의 인공지능 task를 수행할 수있도록 한 것이 심층신경망 혹은 DNN이라고 부른다.



Applications of Deep Learning

  • Computer Vision (영상 인식)
    • Object Detection (객체 인식)
    • Image Synthesis (이미지 합성)
  • Natuaral Laguage Processing(자연어 처리)
  • Time-Series Anlysis(시계열 분석)
  • Reinfrocement Learning(강화 학습)



What is Perceptron?

  • 뉴런의 동작 과정을 수학적으로 본 따서 만든 해당 알고리즘을 구체적으로 perceptron이라고 부른다.
  • perceoptron의 기본적인 동작과정을 살펴보겠다.
    • 다음 퍼셉트론은 두개의 뉴런으로부터 입력신호를 받고 있다.
    • 값을 각각 1,0이라고 할때 가중치와 곱한 뒤 가중합을 계산한다.
    • 또한 상수항도 뉴런의 입력값에 특정한 가중치를 곱하는 방식으로 설명할 수 있다.
    • 이렇게 계산된 값이 0보다 크기때문에 활성함수의 룰에 따라 최종 출력값인 1을 내어주게 된다.

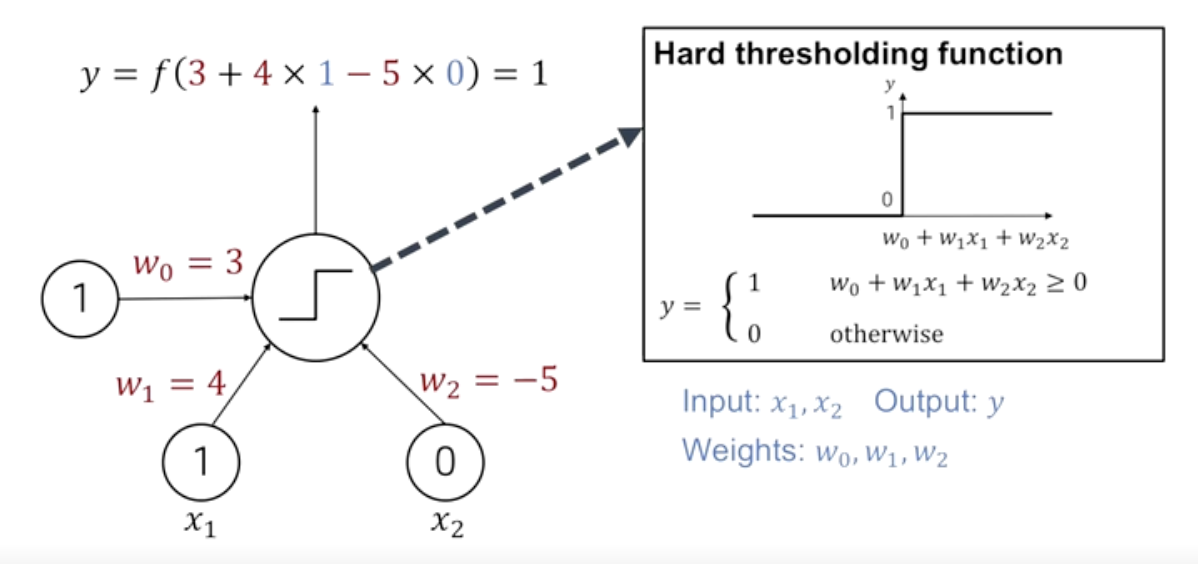
image-20240117163004777


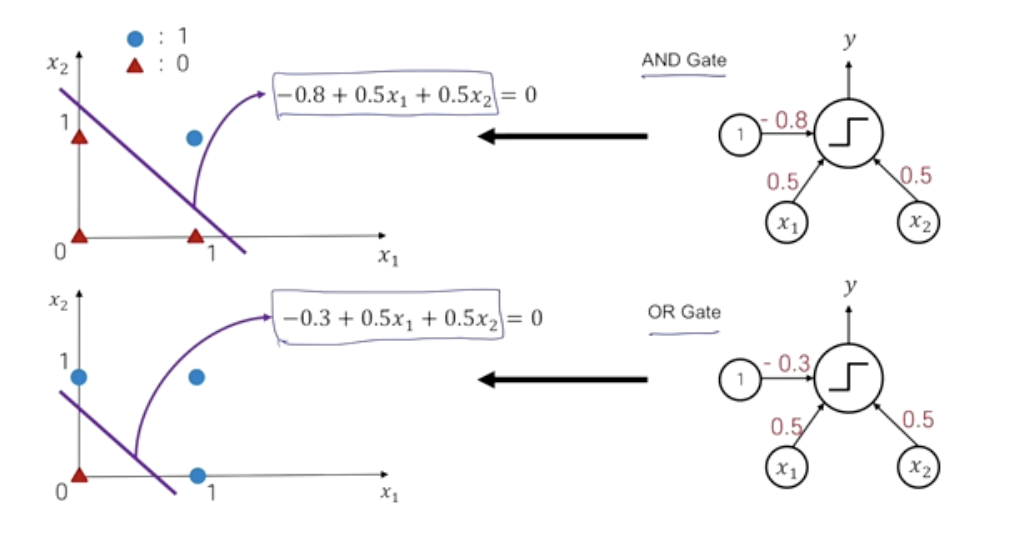
  • And Gate, Or Gate

    • 이렇게 만들어진 perceoptron을 통해 논리 연산에서의 And Or Gate를 쉽게 구현할 수 있다.

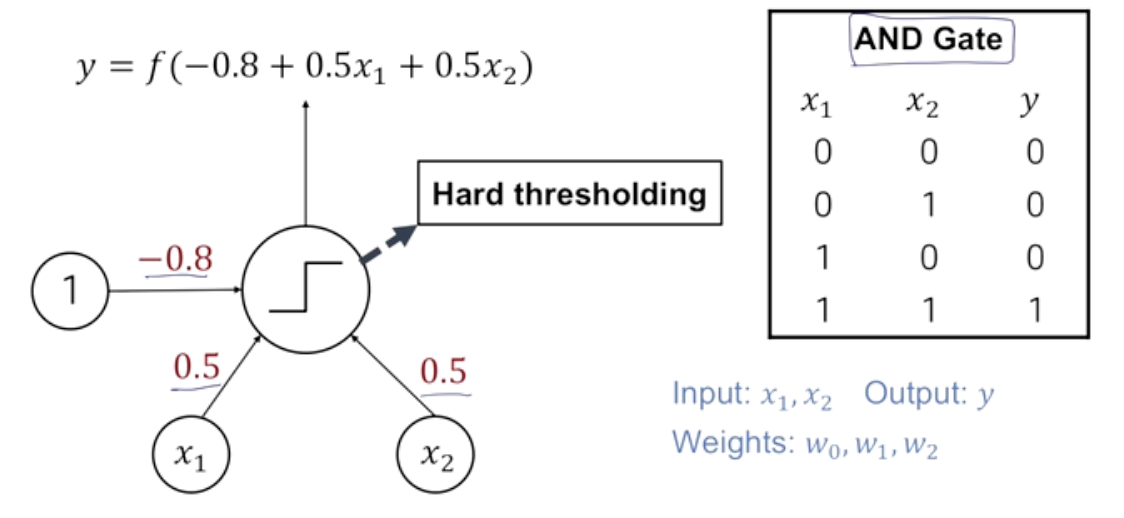
    image-20240117163544555

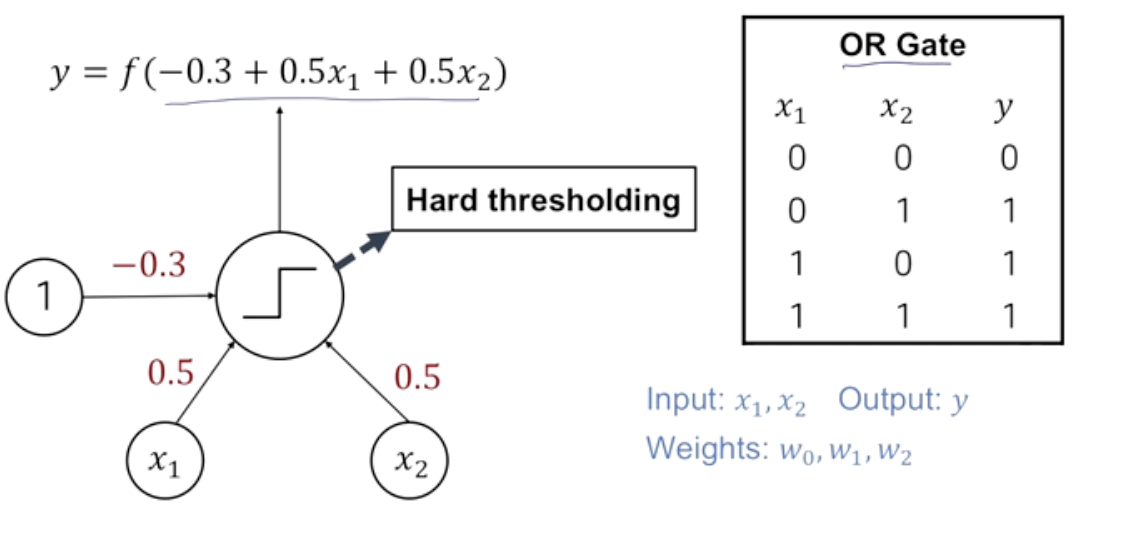
image-20240117163733115



Decision Boundary in Perceptron

  • Decision Boundary
    • AND, OR GATE에서 Perceptron이 위의 활성화 함수처럼 0보다 크면 1 작으면 0으로 표현된다고 할 때 정확히 0을 갖는 지점을 직선으로 그은것을 Decision Boundary라고 한다.
  • Input feature space
    • decision Boundary에 의해서 양분되는 입력 변수의 공간을 뜻한다.

image-20240117164307520



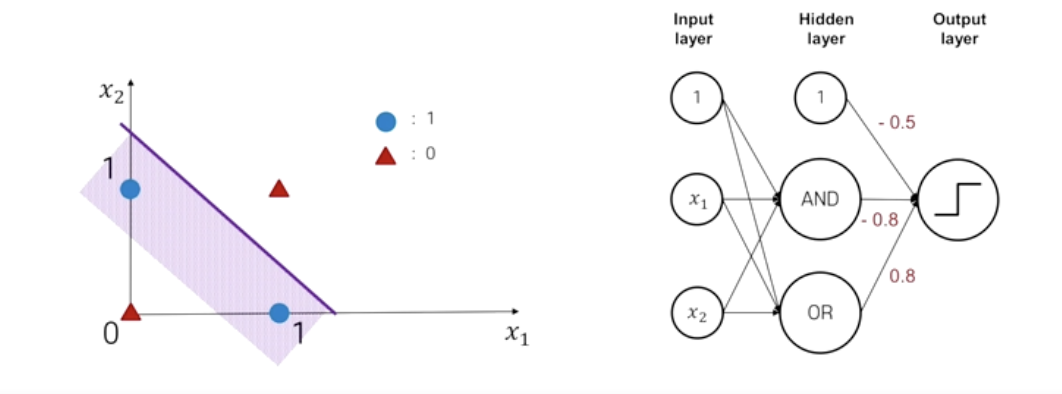
Multi-Layer Perceoptron for XOR Gate

  • XOR Gate
    • 일차함수로는 0,1의 경계를 양분할 수 가 없다.
    • 따라서 여러 단계에 걸쳐서 구성했을 때 가능하게 된다.

image-20240117164714291



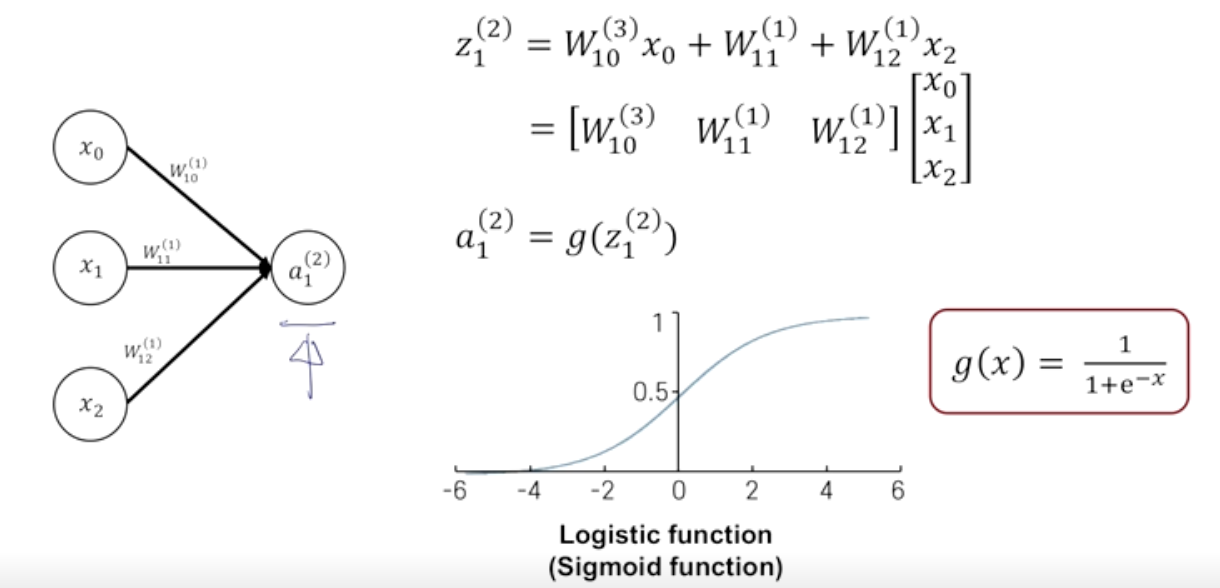
Forward Propagation

  • Forwrad Propagation
    • 여러 계층으로 쌓아진 multi-layer perceptron에서 순차적 계산과정을 나타내는 것이다.

    1. 두가지의 수학적 공식을 정의하게 된다.

      • $a_j^i$ 에서 j는 layer를 뜻하고 i는 몇번째 노드인지를 뜻한다.

      • $w^j$에서 j는 layer를 뜻한다.

    1. 행렬의 내적 형태로 가중합을 나타낼 수 있다.
    2. 아까와는 다르게 부드러운 형태의 로지스틱(시그모이드) 활성화 함수를 거친다.

image-20240117165653956



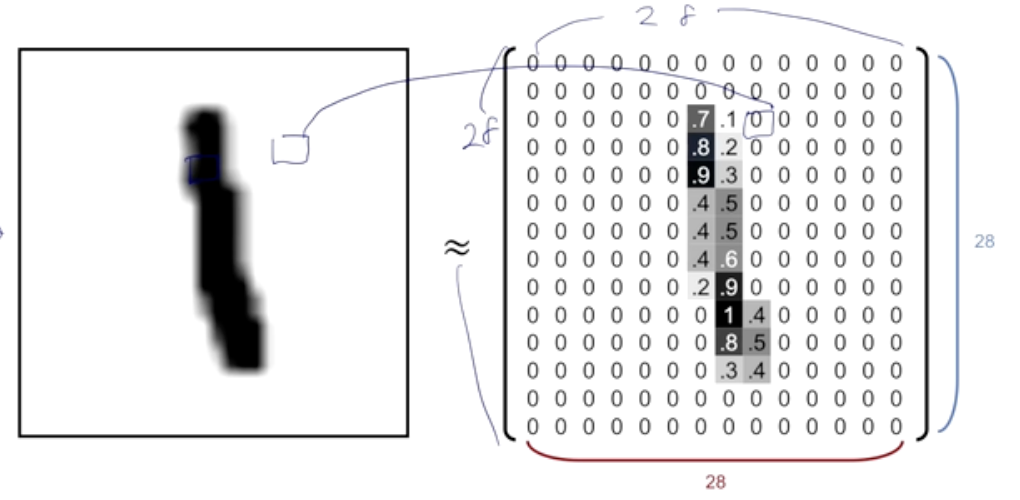
MNIST Dataset

  • 28 * 28 pixel의 이미지가 학습데이터로 55000 , 테스트데이터로 10000 구성되어있다.

image-20240117170059701

  • 검정색에 가까울 수록 1이 되는 형태로 픽셀을 구성하게 된다.

  • 또한 입력 층 구성할 때 28개의 열을 나열하여 28 * 28로 구성한다.

    image-20240117170204990

  • 예측 값과 실제 값의 차이를 제곱 한 값을 합산하는 식으로 loss를 정의 할 수있다.
  • 이러한 Loss 를 mean squared error라고 한다.

image-20240117170554723



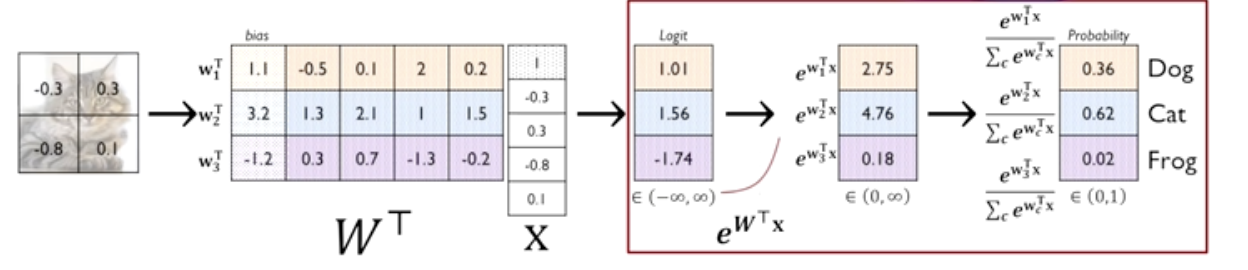
Softmax Layer for Multi-Class Classification

  • 소프트맥스 함수(softmax function)

    • 입력된 값들을 정규화(normalize)하여 출력값을 얻는 활성화 함수 중 하나
    • 이다. 소프트맥스 함수를 사용하면 출력값들의 합이 항상 1이 된다.
    • 이러한 특성 때문에 소프트맥스 함수의 출력은 확률 분포로 해석할 수 있다.

  • 과정을 살펴보자

      1. 그림에서와 같이 행렬의 내적으로 가중합을 표현하게 된다.

      2. 그 후에 나온 값은 -무한대부터 무한대까지의 값으로 표현 할 수 있게 되고

      3. 지수함수를 거쳐서 (0, 무한대) 인 양수의 출력값을 얻게된다.
      4. 최종적으로 모두 다 양수인 값을 가지고 상대적인 비율을 계산하게 된다.
      5. 해석할때는 Dog 일 확률 0.36 처럼 표현하게 된다.

image-20240117171257639

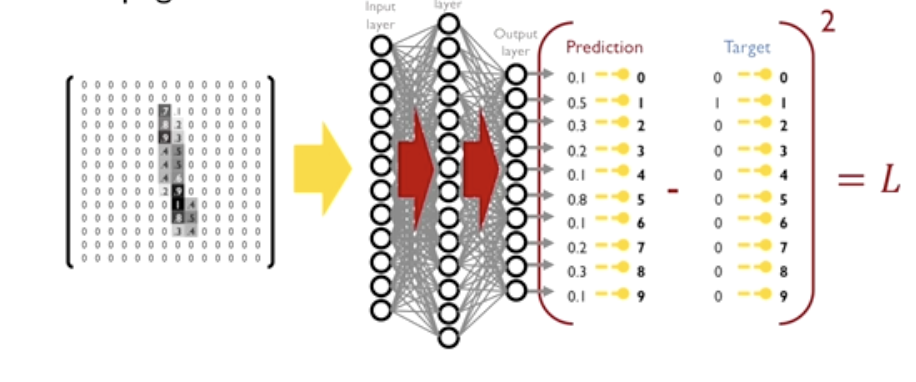
  • Softmax loss(Cross-entropy loss)
    • mse와는 달리 다중 분류 문제에서 소프트맥스에 적용하는 손실함수를 뜻한다.
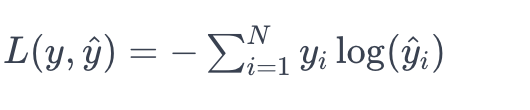
    • image-20240117171851485
    • N은 클래스의 개수이며, y는 실제 클래스의 원-핫 인코딩된 벡터 ( 예제에서는 [0, 1, 0] 형태이다.) , y^는 모델의 소프트맥스 함수를 통과한 예측 확률 분포이다.



CHAPTER 2. Training Neural Network



심층신경망(deep neural networks)의 학습과정

  • neural network의 기본적인 학습 과정
      1. neural network에서 최적화 하고자 하는 파라미터와 학습 데이터를 입력으로 집어넣는다.
      2. loss function을 만들었을 때 loss function을 최소화하는 파라미터를 찾는 과정이다.
      3. 이 Loss function에대해서 각각의 파라미터 들에 미분값을 구한다.
      4. 미분값을 사용하여 현재의 파라미터 값을 미분 방향의 마이너스 방향, 학습률을 곱하여 해당 파라미터를 업데이트한다.
  • original descent algorithm을 그대로 사용 했을 경우 loss function이 복잡한 형태를 띄고 있을 경우 수렴속도가 상대적으로 느린 경우가 생긴다.
    • 따라서 다양한 방식으로 변형 및 개선하는 방법들이 존재한다.



  • MNIST 예제를 살펴보자
    • 학습을 통해 최적화를 이루어 내야 하는 변수인 w, 즉 파라미터들을 업데이트 한다.
      1. 학습 데이터에 대해서 Foward Propagation(순차적 계산과정)을 실행한다.
      2. 이때 사용되는 각 파라미터는 랜덤하게 시작한다.
      3. 손실함수를 차이를 최소화하는 방향으로 구하기 위해
      4. 손실함수에 대한 편미분 값을 구하고 편미분 값을 통해 파라미터를 업데이트 한다.
    • 이때 손실함수에 대해 파라미터를 업데이트 하는것은은 Foward Propagation의 반대 방향으로 진행된다.
      • back Propagation을 통해 w, 파라미터를 업데이트 하게 된다.

image-20240117174012139

Activation Function

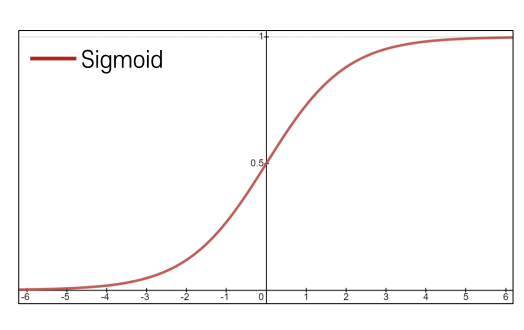
Sigmoid Activation

  • 수식: $( \sigma(x) = \frac{1}{1 + e^{-x}})$
  • 특징:
    • 입력을 (−∞, ∞) 범위에서 [0, 1] 범위로 매핑한다.
    • 입력을 [0, 1]로 변환하여 확률적 해석을 제공해준다.
  • 문제점:
    • Saturated neurons가 그레디언트 소멸 문제 발생한다.
    • 그레디언트 값이 1/4 이하로 감소하여 그레디언트 손실 유발한다.
    • 그러나 saturated 상태에서 그레디언트 소멸 문제가 발생하여 훈련이 어려울 수 있다.

image-20240117180000826


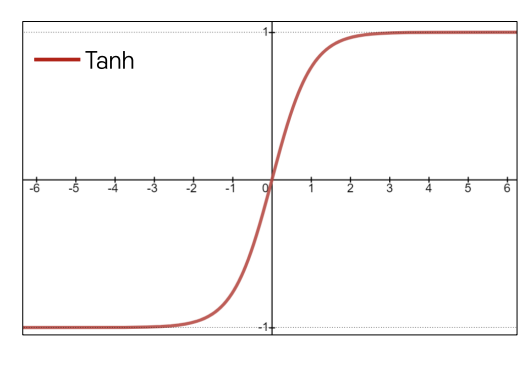
Tanh Activation

  • 수식: $ \tanh(x) = 2 \cdot \sigma(2x) - 1$
  • 특징:
    • [-1, 1] 범위로 수축.
    • Sigmoid의 확장으로 [-1, 1] 범위로 변환하며, Zero-centered 특성을 가진다.
  • 장점:
    • Zero-centered로 평균이 0이라는 특징 제공한다.
  • 단점:
    • 활성화 함수의 출력이 특정 범위에 고정되어 미분 값이 0에 가까워지는 상태에서 그레디언트 소멸 문제 유지된다.

image-20240117180030013


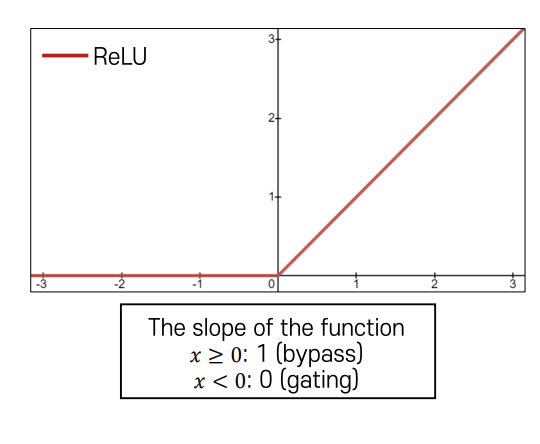
ReLU Activation

  • 수식: $ f(x) = \max(0, x) $
  • 특징:
    • Saturated 되지 않음 (양쪽 영역에서 그레디언트 소멸 문제 해결).
    • 계산 효율적.
  • 장점:
    • Sigmoid나 Tanh에 비해 빠르게 수렴한다.
    • 활성화 함수의 출력이 특정 범위에 고정되어 미분 값이 0에 가까워지는 상태에서도 그레디언트 소멸 문제가 발생하지 않는다.
  • 단점:
    • Zero-centered가 아니며, 입력이 음수인 경우 그레디언트가 완전히 사라진다.

image-20240117180155642

댓글남기기

참고